引言
思考:要经常判断1个元素是否存在,需要怎么做?
Answer:很容易想到哈希表(HashSet、HashMap),元素作为 key 去查找。查找元素过程,使用O(1)时间计算出数组索引(哈希值即为 数组下标),接着每个数组下标指向一颗红黑树(链地址法处理哈希冲突),使用常数级别的时间复杂度去查找对应的value是否存在即可
- 理由:时间复杂度仅为O(1)
- 缺点:空间利用率不高,需要占用比较多的内存资源
需求:如果需要编写一个网络爬虫去爬10亿个网站数据,为了避免爬到重复的网站,如何判断某个网站是否爬过?
- 很显然,HashSet、HashMap 并不是非常好的选择,需要占用大量空间
- 是否存在时间复杂度低、占用内存较少的方案?
- 布隆过滤器(Bloom Filter)
布隆过滤器简介
1970年由布隆提出的一种数据结构。它是一个 空间效率高的概率型数据结构。
作用:判断一个元素 一定不存在 或者 可能存在
优缺点:
- 优点:空间效率 和 查询时间都远远超过 一般算法
- 缺点:有一定的误判率、删除困难
布隆过滤器的本质:实际上是一个很长的二进制向量 和 一系列随机映射函数(Hash函数)
常见应用:网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统、解决缓存穿透问题
应用布隆过滤器的需求场景
- 需要判断某个元素是否存在
- 元素数量巨大,希望用比较少的内存空间
- 允许有一定的误判率
布隆过滤器原理
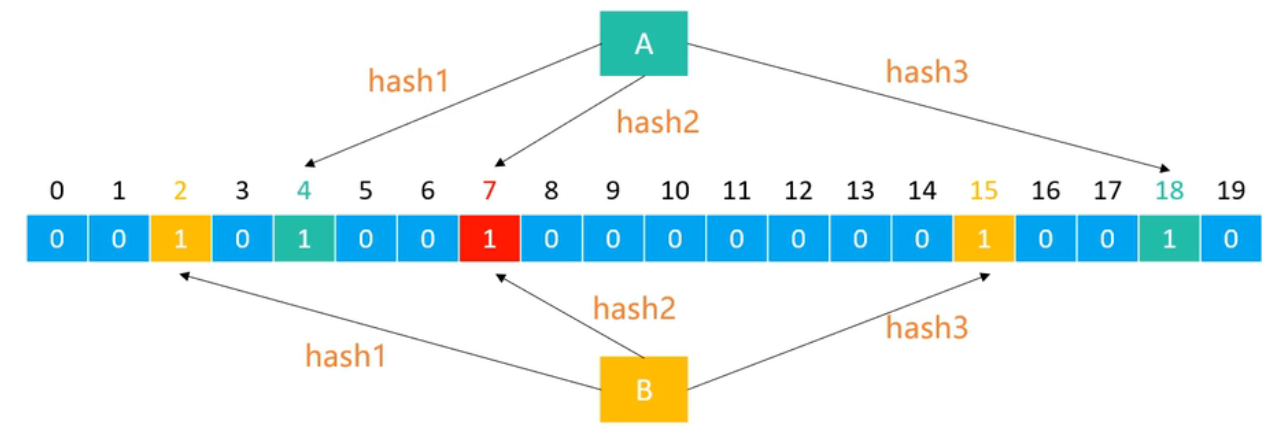
假设: 布隆过滤器由 20位二进制、 3 个哈希函数组成,每个元素经过哈希函数处理都能生成一个索引位置
- 添加元素:将每一个哈希函数生成的索引位置都设为 1
- 查询元素是否存在
- 如果有一个哈希函数生成的索引位置不为 1,就代表不存在(100%准确)
- 如果每一个哈希函数生成的索引位置都为 1,就代表可能存在(存在一定的误判率)
复杂度分析
-
添加、查询时间复杂度:O(k),k为 哈希函数个数
-
空间复杂度:O(m),m是二进制位的个数
布隆过滤器误判率
布隆过滤器实现
附录
参考文献
版权信息
本文原载于kitebin.top,遵循CC BY-NC-SA 4.0协议,复制请保留原文出处。