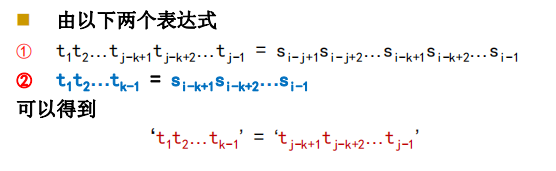线性结构

线性表

线性表的抽象数据类型

ADT 线性表(List)

Data Description

线性表的数据对象集合为 {a₁, a₂, ……, a_n}，每个元素的类型为 DataType。其中除了首个元素a₁外，每个元素有且仅有一个直接前驱元素，除了最后一个元素a_n外，每个元素有且仅有一个直接后继元素。数据元素之间的关系是一对一关系。

Operation

InitList(* L) ：初始化操作，建立一个空的线性表L

ListEmpty(L)：若是线性表为空，返回 true；否则返回 false

ClearList(* L) ：将线性表清空

GetElem(L, i, * elem)：将线性表L中第i个位置元素值返回给elem

LocateElem(L, elem)：在线性表L中查找与给定值elem相等(只查找第一个相等元素)的元素。若是查找成功，返回该元素在表中序号表示成功；否则，返回 -1表示失败。

ListInsert(* L, i , elem)：在线性表L中的第i个有位置插入新元素elem

ListDelete(* L, i, * elem)：删除线性表L中第i个位置元素，并用elem返回其值

ListLength(L)：返回线性表L的元素个数

endADT

顺序表

线性表的顺序存储结构：用一段地址连续的存储单元一次存储线性表的数据元素。

提示：一个实现方式，可以用一维数组来实现顺序存储结构。

线性表顺序存储结构代码

1
2
3
4
5
6


#define MAXSIZE 20      /* 存储空间初始分配量 */
typedef int ElemType;   /* ElemType类型可以根据实际情况而定，这里为int */
typedef struct {
	  ElemType data[MAXSIZE];   /* 数组，存储数据元素 */ 
	  int len;   /* 线性表当前长度 */
}SqList;

可以发现顺序存储结构只需要描述三个属性：

存储空间的起始位置：数组data，其存储位置就是存储空间的存储位置
线性表的最大存储容量：数组长度为MAXSIZE
线性表当前的长度：len

顺序存储结构的插入与删除

获得元素操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


#define OK 1
#define ERROR 0
/* Status是函数原型，其值为函数结构状态代码，如OK等 */
typedef int Status;

Status GetElem(SqList L, int i, ElemType *e) {
	if (L.len == 0 || i < 1 || i > L.len) {
		return ERROR;
	}
	*e = L.data[i-1];
	return OK;
}

插入操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


/* 初始条件：顺序线性表L已存在，1 <= i <= ListLen(L) */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
Status ListInsert(SqList *L, int i, ElemType e) {
	int k;
	if (L->len == MAXSIZE) /* 顺序线性表容量已满 */
		return ERROR;
	if (i < 1 || i > L->len+1) /* 当i比第一位置小或 比最后一位+1还要大 */
		return ERROR;
	for (k = L->len-1; k >= i-1; k--) /* 将要插入位置后的元素后移一位 */
		L->data[k+1] = L->data[k];
	L->data[i-1] = e; /*  插入新的元素 */
	L->len++;

	return OK;
}

删除操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


/* 初始条件：顺序线性表L已存在，1<= i <= Listlen(L) */
/* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
Status ListDelete(SqList *L, int i, ElemType *e) {
	int k;
	if (L->len == 0)
		return ERROR;   /* 线性表为空 */
	if (i < 1 || i > L->len) 
		return ERROR;    /* 删除位置不正确 */
	*e = L->data[i-1];   // 获取删除元素
	for (k = i; k < L->len; k++) {  /* 将删除位置的后继元素前移 */
		L->data[k-1] = L->data[k];
	}
	L->len--;
	return OK;
}

顺序表类实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66


class SqList {  
private:  
    int len;  
    int* data;  
    int maxSize;  
public:  
    SqList(int maxSize) {  
        this->len = 0;  
        this->maxSize = maxSize;  
        data = new int[maxSize];  
    }  
    ~SqList() {  
        this->len = 0;  
        delete[] data;  
    }  
    bool isEmpty() {  
        if (len == 0) {  
            return true;  
        } else {  
            return false;  
        }  
    }  
    void clear() {  
        this->len = 0;  
    }  
    // 传入的pos范围[0, len)  
    int getElem(int pos, int* elem) {  
        if (len == 0 || pos < 0 || pos > len-1)  
            return -1;  
        *elem = data[pos];  
        return 0;  
    }  
    int getLen() {  
        return this->len;  
    }  
    // 函数返回元素在数组中下标序号，范围为[0, len)  
    int elemLocate(int elem) {  
        for (int i = 0; i < len; i++) {  
            if (elem == data[i])  
                return i;  
        }  
        return -1;  
    }  
    // data数组实际数据下标范围[0, len)  
    int listInsert(int pos, int elem) {  
        if (pos < 0 || pos > len || len >= maxSize)  
            return -1;  
        // 包含了 线性表尾插和中间元素插入 两种情况
        for (int i = len-1; i > pos-1; i--) {  
            data[i+1] = data[i];  
        }  
        data[pos] = elem;  
        this->len++;  
        return 0;  
    }  
    // data数组实际数据下标范围[0, len)  
    int listDelete(int pos) {  
        if (pos < 0 || pos > len || len == 0)  
            return -1;  
        for (int i = pos; i < len-1; i++) {  
            data[i] = data[i+1];  
        }  
        this->len--;  
        return 0;  
    }  
};

DS顺序表—存储结构与操作

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134


#include <iostream>  
  
using namespace std;  
  
class SqList {  
private:  
    int len;  
    int* data;  
    int maxSize;  
public:  
    SqList(int maxSize) {  
        this->len = 0;  
        this->maxSize = maxSize;  
        data = new int[maxSize];
    }  
    ~SqList() {  
        this->len = 0;  
        delete[] data;  
        data = nullptr;  
    }  
    bool isEmpty() {  
        if (len == 0) {  
            return true;  
        } else {  
            return false;  
        }  
    }  
    void clear() {  
        this->len = 0;  
    }  
    // 传入的pos范围[0, len)  
    int getElem(int pos, int* elem) {  
        if (len == 0 || pos < 0 || pos > len-1)  
            return -1;  
        *elem = data[pos];  
        return 0;  
    }  
    int getLen() {  
        return this->len;  
    }  
    // 函数返回元素在数组中下标序号，范围为[0, len)  
    int elemLocate(int elem) {  
        for (int i = 0; i < len; i++) {  
            if (elem == data[i])  
                return i;  
        }  
        return -1;  
    }  
    // data数组实际数据下标范围[0, len)  
    int listInsert(int pos, int elem) {  
        if (pos < 0 || pos > len || len >= maxSize)  
            return -1;  
        for (int i = len-1; i > pos-1; i--) {  
            data[i+1] = data[i];  
        }  
        data[pos] = elem;  
        this->len++;  
        return 0;  
    }  
    // data数组实际数据下标范围[0, len)  
    int listDelete(int pos) {  
        if (pos < 0 || pos > len || len == 0)  
            return -1;  
        for (int i = pos; i < len-1; i++) {  
            data[i] = data[i+1];  
        }  
        this->len--;  
        return 0;  
    }  
    void display() {  
        cout << this->len << " ";  
        for (int i = 0; i < len; i++)  
            cout << data[i] << " ";  
        cout << endl;  
    }  
};  
  
  
int main() {  
    int n;  
    cin >> n;  
  
    SqList sqList(1000);  
  
    int val;  
    for (int i = 0; i < n; i++) {  
        cin >> val;  
        sqList.listInsert(i, val);  
    }  
    sqList.display();  
  
    // 插入操作  
    int pos;  
    cin >> pos >> val;  
    if (sqList.listInsert(pos-1, val) == -1) {  
        cout << "error" << endl;  
    } else {  
        sqList.display();  
    }  
    cin >> pos >> val;  
    if (sqList.listInsert(pos-1, val) == -1) {  
        cout << "error" << endl;  
    } else {  
        sqList.display();  
    }  
  
    // 删除操作  
    cin >> pos;  
    if (sqList.listDelete(pos-1) == -1) {  
        cout << "error" << endl;  
    } else {  
        sqList.display();  
    }  
    cin >> pos;  
    if (sqList.listDelete(pos-1) == -1) {  
        cout << "error" << endl;  
    } else {  
        sqList.display();  
    }  
  
    // 查找  
    cin >> pos;  
    if (sqList.getElem(pos-1, &val) == -1) {  
        cout << "error" << endl;  
    } else {  
        cout << val << endl;  
    }  
    cin >> pos;  
    if (sqList.getElem(pos-1, &val) == -1) {  
        cout << "error" << endl;  
    } else {  
        cout << val << endl;  
    }  
}

单链表

线性表的链式存储结构：用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。

存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成数据元素a_i 的存储映像，称为结点(Node)。

单链表：n个结点(a_i 的存储映像)链接成一个链表，即为线性表(a₁ , a₂ , … , a_n ) 的链式存储结构。由于链表的每个结点只包含一个指针域，所以叫做单链表。

头指针与头结点异同

头指针：链表中的第一个结点的存储位置。

头结点：一般为了更方便对链表进行操作，会在单链表的第一个结点前附设一个结点，称为头结点。

头指针

指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针
头指针具有标志作用，常用头指针冠以链表的名字
无论链表是否为空，头指针均不为空。头指针是链表的必要元素。

注：对于线性表来说，描述的元素莫过于如何定义线性表的头和尾，在链表中这个头就是头指针，而在顺序表中，这个头指的是数组data第一个元素。在链表中，这个尾部即可以添加一个游标cur来表示，也可以用长度len表示；而顺序表中，这个尾部可以用长度len表示。

头结点

头结点是为了操作的统一和方便而设立的，放在第一个实际元素的结点之前，其数据域一般无意义(也可以存放链表的长度)
有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其他结点的操作统一了
头结点不是链表的必需要素

线性表链式存储结构代码

1
2
3
4
5
6


/* 线性表的单链表存储结构 */
typedef struct Node {
	ElemType data;
	struct Node *next;
}Node;
typedef struct Node *LinkList; /* 定义LinkList */

单链表的读取

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


/* 初始条件：链式线性表L已存在，1 <= i <= ListLength(L) */
/* 操作结果：用e返回L中第i个数据元素的值 */
Status GetElem(LinkList L, int i, ElemType *e) {
	int j;   
	LinkList p;   // Node指针
	p = L->next;  // 让p指向链表L的第一个结点
	j = 1; // j为计数器
	while (p && j < i) {
		p = p->next;    // p指向下一个结点
		++j;
	}
	// p = nullptr 说明链表没有第i个元素 此时 j < i
	// j > i，说明是乱写的 不需要这个条件 若是链表中有环，那么也不会有 j > i情况
	if (!p)  return ERROR;
	*e = p->data;  // 取第i个元素数据
	return OK;
}

时间复杂度：O(N)

注：由于单链表中没有定义表长，不能事先知道要循环的次数，不方便使用for控制循环。这里的核心思想：“工作指针后移”。

单链表的插入与删除

单链表的插入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


/* 初始条件：链式线性表L已存在，1 <= i <= ListLength(L) */
/* 操作结果：在L中第i个位置之前 插入新的数据元素e，L的长度加1 */
Status ListInsert(LinkList *L, int i, ElemType e) {
	int j;
	LinkList p, s;
	// LinkList为 Node指针，LinkList* L，则L为 Node二级指针，这里的p需要解引用，得到实际的 L链表头指针
	p = *L;
	j = 1;
	// 查找第 i-1位置元素
	while (p && j < i) {
		p = p->next;
		j++;
	}
	if (!p) {
		return ERROR; // 第i个元素不存在
	}
	s = (LinkList)malloc(sizeof(Node));
	s->data = e;
	// 核心插入结点操作，其中 p 为第 i-1 个有效的结点指针
	s->next = p->next;  // 将 原来第i个结点地址 赋值给s的后继
	p->next = s;   // 将原来 第i-1结点后继结点 指向 s
	return OK;
}

单链表的删除

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


/* 初始条件：链式线性表L已存在，1 <= i <= ListLength(L) */
/* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
Status ListDelete(LinkList *L, int i, ElemType *e) {
	int j;
	LinkList p, q;
	p = *L;
	j = 1;
	while (p->next && j < i) {  // 遍历寻找第i个元素
		p = p->next;
		j++;
	}
	if (!(p->next)) { // 此时 j < i，且说明第i个元素不存在
		return ERROR;
	}
	q = p->next;   
	p->next = q->next;   // 将q的后继赋值给p的后继
	*e = q->data;   // 将q结点中的数据赋值给 e
	free(q);   // 系统回收结点，释放内存
	return OK;
}

单链表的整表创建

头插法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


/* 随机产生n个元素的值，建立带表头结点的单链线性表L(头插法) */
void CreateListHead(LinkList *L, int n) {
	LinkList p;
	int i;
	srand(time(0)); // 初始化随机种子
	*L = (LinkList)malloc(sizeof(Node));
	(*L)->next = NULL;   // 建立一个带头结点的单链表
	for (i = 0; i < n; i++) {
		p = (LinkList)malloc(sizeof(Node));  // 生成新结点
		p->data = rand()%100 + 1;    // 随机生成100以内的正整数 
		p->next = (*L)->next;
		(*L)->next = p;     // 插入到表头
	}
}

尾插法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


/*  随机产生n个元素的值，建立带表头结点的单链线性表L (尾插法) */
// 函数内使用两个游标 r, p分别指向链表最后一个结点 和 新创建的结点
// 那最后的创建好的头指针怎么表示？
// 关键在于函数参数设置：这里传入的参数是 LinkList*L指针，就是说，在函数外部的是对于头指针取地址，头指针并不会改变
void CreateListTail(LinkList *L, int n) {
	LinkList p, r;
	int i;
	srand(time(0));  // 初始化随机种子
	*L = (LinkList)malloc(sizeof(Node));   // L为整个线性表
	r = *L;
	for (int i = 0; i < n; i++) {
		p = (Node*)malloc(sizeof(Node));   // 生成新结点
		p->data = rand()%100 + 1; // 生成100以内随机整数
		r->next = p;  // 将表尾终端结点的指针指向新结点
		r = p;      // 将当前的新结点定义为 表位终端结点
	}
	r->next = nullptr; // 表示当前链表结束
}

单链表的整表删除

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


/* 初始条件：链式线性表L已存在。操作结果：将L重置为空表 */
Status ClearList(LinkList *L) {
	LinkList p, q;
	p = (*L)->next;   // p指向第一个结点
	while (p) {
		q = p->next;
		free(p);
		p = q;
	}
	*(L)->next = nullptr;  // 头结点指针域指向空
	return OK;
}

单链表结构与顺序存储结构优缺点

存储分配方式

顺序存储结构：用一段连续存储单元一次存储线性表的数据元素
单链表：采用链式存储结构，用一组任意的存储单元存放线性表的元素

时间性能

查找
- 顺序存储O(1)
- 单链表O(n)
插入和删除
- 顺序存储结构：平均移动表长一半元素，时间复杂度O(n)
- 单链表：找出位置后，插入和删除O(1)

空间性能

顺序存储结构：需要预分配存储空间，不好控制
单链表：不需要预先分配存储空间

小结：

线性表需要频繁查找，很少进行插入或删除操作时，宜采用顺序存储结构
线性表中的元素个数变化较大时，宜采用单链表结构

单链表类实现

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125


struct ListNode {  
    int data;  
    ListNode* next;  
};  
  
class Linklist {  
private:  
    ListNode *head;  
    int len;  
public:  
    Linklist() {  
        this->len = 0;  
        this->head = new ListNode; // 构建头结点  
        this->head->next = nullptr;  
    }  
    ~Linklist() {  
        ListNode* p, *q;  
        p = head;  
        while (p) {  
            q = p->next;  
            delete p;  
            p = q;  
        }  
        head = nullptr;  
        len = 0;  
    }  
    bool isEmpty() {  
        if (this->len)  
            return false;  
        else  
            return true;  
    }  
    // pos 传入实际的位置坐标 1~len    ListNode* getElem(int pos) {  
        ListNode* p = head->next;  
        int j = 1; // 计数器  
        if (pos < 1 || pos > len) return nullptr;  
        // 一般有pos > len判断 下面的p不会出现 nullptr情况 不过还是特判一下防止访问非法内存  
        while (p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        return p;  
    }  
    int getLen() {  
        return this->len;  
    }  
    // 头插法创建  
    void createListHead(const int arr[], int n) {  
        ListNode *p, *q;  
        int j = 0;  
        p = this->head;  
        while (j < n) {  
            q = new ListNode;  
            q->data = arr[j];  
            q->next = p->next;  
            p->next = q;  
            j++; len++;  
        }  
    }  
  
    // 尾插法创建  
    void createListTail(const int arr[], int n) {  
        ListNode *p, *q;  
        int j = 0;  
        p = this->head;  
        while (j < n) {  
            q = new ListNode;  
            q->data = arr[j];  
            p->next = q;  
            p = q;  
            j++; len++;  
        }  
        p->next = nullptr;  
    }  
    // 插入某个结点  
    int listInsert(int pos, int val) {  
        // 插入 结点 可以插入到len+1位置  
        if (pos < 1 || pos > len+1)  
            return -1;  
        ListNode *p = this->head;  
        int j = 1; // 计数器  
        // 找到 第 pos-1 个位置的结点  
        while(p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        ListNode *q = p->next;  
        ListNode *s = new ListNode;  
        s->data = val;  
        s->next = q;  
        p->next = s;  
        len++;  
        return 0;  
    }  
    // 删除某个结点  
    int listDelete(int pos) {  
        if (pos < 1 || pos > len) {  
            return -1;  
        }  
        ListNode *p = this->head;  
        int j = 1; // 计数器  
        // 找到 第 pos-1 个位置  
        while (p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        ListNode *q = p->next;  
        p->next = q->next;  
        delete q;  
        len--;  
        return 0;  
    }  
    // 整表删除  
    void clearList() {  
        ListNode *p, *q;  
        p = this->head;  
        while (p) {  
            q = p->next;  
            delete p;  
            p = q;  
        }  
        len = 0;
        this->head = nullptr;  
    }  
};

DS单链表–存储结构与操作

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202


#include <iostream>  
  
using namespace std;  
  
const int N = 1001;  
int arr[N];  
  
struct ListNode {  
    int data;  
    ListNode* next;  
};  
  
class Linklist {  
private:  
    ListNode *head;  
    int len;  
public:  
    Linklist() {  
        this->len = 0;  
        this->head = new ListNode; // 构建头结点  
        this->head->next = nullptr;  
    }  
    ~Linklist() {  
        ListNode* p, *q;  
        p = head;  
        while (p) {  
            q = p->next;  
            delete p;  
            p = q;  
        }  
        head = nullptr;  
        len = 0;  
    }  
    bool isEmpty() {  
        if (this->len)  
            return false;  
        else  
            return true;  
    }  
    // pos 传入实际的位置坐标 1~len    ListNode* getElem(int pos) {  
        ListNode* p = head->next;  
        int j = 1; // 计数器  
        if (pos < 1 || pos > len) return nullptr;  
        // 一般有pos > len判断 下面的p不会出现 nullptr情况 不过还是特判一下防止访问非法内存  
        while (p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        return p;  
    }  
    int getLen() {  
        return this->len;  
    }  
  
    // 头插法创建  
    void createListHead(const int arr[], int n) {  
        ListNode *p, *q;  
        int j = 0;  
        p = this->head;  
        while (j < n) {  
            q = new ListNode;  
            q->data = arr[j];  
            q->next = p->next;  
            p->next = q;  
            j++; len++;  
        }  
    }  
  
    // 尾插法创建  
    void createListTail(const int arr[], int n) {  
        ListNode *p, *q;  
        int j = 0;  
        p = this->head;  
        while (j < n) {  
            q = new ListNode;  
            q->data = arr[j];  
            p->next = q;  
            p = q;  
            j++; len++;  
        }  
        p->next = nullptr;  
    }  
  
    // 插入某个结点  
    int listInsert(int pos, int val) {  
        // 插入 结点 可以插入到len+1位置  
        if (pos < 1 || pos > len+1)  
            return -1;  
        ListNode *p = this->head;  
        int j = 1; // 计数器  
        // 找到 第 pos-1 个位置的结点  
        while(p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        ListNode *q = p->next;  
        ListNode *s = new ListNode;  
        s->data = val;  
        s->next = q;  
        p->next = s;  
        len++;  
        return 0;  
    }  
  
    // 删除某个结点  
    int listDelete(int pos) {  
        if (pos < 1 || pos > len) {  
            return -1;  
        }  
        ListNode *p = this->head;  
        int j = 1; // 计数器  
        // 找到 第 pos-1 个位置  
        while (p && j < pos) {  
            p = p->next;  
            j++;  
        }  
        ListNode *q = p->next;  
        p->next = q->next;  
        delete q;  
        len--;  
        return 0;  
    }  
  
    // 整表删除  
    void clearList() {  
        ListNode *p, *q;  
        p = this->head;  
        while (p) {  
            q = p->next;  
            delete p;  
            p = q;  
        }  
        len = 0;
        this->head = nullptr;  
    }  
  
    // 输出单链表内容  
    void display() {  
        ListNode* p = head->next;  
        int j = 0;  
        while (p && j < len) {  
            cout << p->data << " ";  
            p = p->next;  
        }  
        cout << "\n";  
    }  
};  
  
int main() {  
    int n;  
    cin >> n;  
    int val;  
    for (int i = 0; i < n; i++) {  
        cin >> val;  
        arr[i] = val;  
    }  
    Linklist myList;  
    myList.createListTail(arr, n);  
    myList.display();  
    int pos;  
    // 插入数据  
    cin >> pos >> val;  
    if (myList.listInsert(pos, val) == -1) {  
        cout << "error\n";  
    } else {  
        myList.display();  
    }  
    cin >> pos >> val;  
    if (myList.listInsert(pos, val) == -1) {  
        cout << "error\n";  
    } else {  
        myList.display();  
    }  
    // 删除数据  
    cin >> pos;  
    if (myList.listDelete(pos) == -1) {  
        cout << "error\n";  
    } else {  
        myList.display();  
    }  
    cin >> pos;  
    if (myList.listDelete(pos) == -1) {  
        cout << "error\n";  
    } else {  
        myList.display();  
    }  
    // 查找位置  
    ListNode* p;  
    cin >> pos;  
    if ((p = myList.getElem(pos)) == nullptr) {  
        cout << "error\n";  
    } else {  
        cout << p->data << "\n";  
    }  
    cin >> pos;  
    if ((p = myList.getElem(pos)) == nullptr) {  
        cout << "error\n";  
    } else {  
        cout << p->data << "\n";  
    }  
    return 0;  
}

静态链表

数组代替指针描述单链表。

静态链表存储结构

1
2
3
4
5
6


#define MAXSIZE 1000   /* 存储空间初始分配量 */
/* 线性表的静态链表存储结构 */
typedef struct {
	ElemType data;
	int cur;    /* 游标(cursor)，为0时表示无指向 */
}Component, StaticLinkList[MAXSIZE];

可以对数组的第一个和最后一个元素作 特殊元素处理，不存放实际数据。我们通常把未被使用的数组元素称为备用链表。

数组第一个元素：下标为0，cur存放备用链表的第一个结点下标

数组最后一个元素：存放第一个有数值的元素的下标，相当于单链表中的头结点作用。当整个链表为空时，则为0。

注意：静态链表中，默认cur为0代表着当前的结点指向的是nullptr。

静态链表初始化

1
2
3
4
5
6
7
8
9


/* 将一维数组space 中各分量链成一个备用链表，space[0].cur为头指针，其中定义"0"为空指针 */
Status InitList(StaticLinkList space) {
	int i;
	for (i = 0; i < MAXSIZE-1; i++) {
		space[i].cur = i+1;
	}
	space[MAXSIZE-1] = 0; /* 静态链表此时为空，最后一个元素的cur为0 */
	return OK;
}

静态链表的插入操作

静态链表解决问题：如何用静态模拟动态链表的结构的存储空间的分配，需要时申请，无用时释放。

动态链表与静态链表差异：

动态链表中，结点的申请和释放分别借用 malloc() 和 free() 函数实现
静态链表中，操作的是数组，不存在动态链表的结点申请和释放问题，需要手动模拟实现类似上面两个函数的功能

静态链表空闲空间管理：把所有未被使用过的及已经被删除的分量用游标链成一个备用链表。每当进行插入时，从备用链表中取得第一个结点作为待插入的新结点。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


/* 若备用空间链表非空，则返回分配的结点下标，否则返回0 */
int Malloc_SSL(StaticLinkList space) {
	int i = space[0].cur;    // 当前数组第一个元素的cur存的值
	if (space[0].cur)
		space[0].cur = space[i].cur;    // 将数组下标为0 的cur指向下一个可用的空间下标
	
	return i;
}

Status ListInsert(StaticLinkList L, int i, ElemType e) {
	int j, k, l;
	k = MAXSIZE - 1;   // 注意 k 首先是最后一个元素的下标
	if (i < 1 || i > ListLength(L)+1)   
		return ERROR;
	j = Malloc_SSL(L);   // 获得空闲分量的下标
	if (j) {
		L[j].data = e;    // 将数据赋值给此分量的 data
		// k为数组最后一个下标，为静态链表的头结点，L[k].cur指向已经分配链表的头结点
		for (l = 1; l <= i-1; l++)  // l 作为计数器，找到第i个元素前一个位置
			k = L[k].cur;
	// 注：这里说明一点
	// 当 i = 1，也就是边界情况，此时 i-1个元素时不存在的，要插入第一个元素，那么上面的循环找第i-1个元素也就不会进入
	// 此时的 L[k].cur = 0，代表着 已分配链表中，头指针指向了 nullptr (这里下标 0 的含义)
	// 那么 L[j].cur = L[k].cur = 0，也就是第一个插入元素后继元素指向 nullptr
	// 而 L[k].cur = j，即下标为 j 的数组元素存储着已分配链表的 第一个元素
	// 故这里的边界情况处理和正常情况统一了
		L[j].cur = L[k].cur;  // 把第i-1个元素的cur赋值给新元素的cur
		L[k].cur = j;    // 把新元素的下标 赋值给 第i-1个元素的cur
		return OK;
	}
	return ERROR;
}

静态链表的删除操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


Status ListDelete(StaticLinkList L, int i) {
	int j, k;
	if (i < 1 || i > ListLength(L))
		return ERROR;
	k = MAXSIZE - 1;
	for (j = 1; j <= i-1; j++) {
		k = L[k].cur;
	}
	j = L[k].cur;
	L[k].cur = L[j].cur;
	Free_SSL(L, j);
	return OK;
}

/* 将下标为k的空闲结点回收到备用链表 */
void Free_SSL(StaticLinkList space, int k) {
	space[k].cur = space[0].cur;   // 把第一个元素的cur值 赋给要删除的分量cur
	space[0].cur = k;    // 把要删除的分量下标赋值给第一个元素的cur
}

静态链表其他操作与单链表类似，下面实现ListLength：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


/* 初始条件：静态链表L已存在。操作结果：返回L中数据元素的个数 */
int ListLength(StaticLinkList L) {
	int j = 0;  // 计数器
	int i = L[MAXSIZE-1].cur;   // 已分配空间的单链表头指针
	while(i) {
		i = L[i].cur;
		j++;  // 统计实际元素个数
	}
	return j;
}

静态链表的优缺点

优点

在插入与删除操作时，只需要修改游标，不需要移动元素，从而改进了在顺序存储结构中插入和删除操作需要移动大量元素的缺点

缺点

没有解决连续存储分配带来的表长难以确定的问题。失去了链式存储结构随机存取的特性。

小结

静态链表一般是为了给没有指针的高级语言设计的一种实现单链表能力的方法。当然，在算法竞赛中，由于静态链表使用数组模拟单链表可以减少动态申请、删除内存所带来的时间性能损耗，运行效率比较高效。

循环链表

循环链表(circular linked list)：将单链表中终端结点的指针端由空指针改为指向头结点，使得整个单链表形成一个环，这种头尾相接的单链表称为单循环链表。

循环链表解决的问题：如何从任意一个结点出发，访问到链表的全部结点。

头结点设置：为了空链表与非空链表处理一致。

循环链表与单链表差异

循环判断条件转换

1
2
3
4
5


// 单链表
while (p->next != NULL);

// 循环链表
while (p->next != head)

改造循环链表

1
2
3
4
5
6
7


/* 线性表的单链表存储结构 */
typedef struct Node {
	ElemType data;
	struct Node *next;
}Node;
typedef struct Node *rearA; /* 定义循环链表的尾指针 代表整个循环链表 */
typedef struct Node *headA;  // 原始定义头指针

头指针代表循环链表或尾指针代表循环链表区别

尾指针：访问最后一个结点，时间复杂度O(1)；访问第一个结点，时间复杂度O(1)
头指针：访问第一个结点，时间复杂度O(1)；访问最后一个结点，时间复杂度O(n)

尾指针代表循环链表例子

将两个循环链表合并成一个表

1
2
3
4
5
6


p = rearA->next;   // 保存A表的头结点
rearA->next = rearB->next->next;   // 将A表尾指针 指向 B表的第一个结点(不是头结点)

q = rearB->next;   
rearB->next = p;   // 将B表尾指针 指向 A表头结点
free(q);       // 释放B表本来的头结点

双向链表

存储结构

1
2
3
4
5
6


/* 线性表的双向链表存储结构 */
typedef struct DulNode{
	ElemType data;
	struct DulNode *prior;  // 直接前驱指针
	struct DulNode *next;   // 直接后继指针
}DulNode, *DuLinkList;

双向链表中，某一结点p，它的后继的前驱是自己，它的前驱的后继也是自己，即：

1

p->next->prior = p = p->prior->next

双向链表中与单链表相同的操作

ListLength：求长度
GetElem：查找元素
LocateElem：获得元素位置

注：上述这些操作，只涉及到一个方向的指针。

插入与删除操作

插入

1
2
3
4
5


// 将存储元素e 的结点s 插入到 结点p和p->next之间
s->prior = p;  // 把p赋值给s的前驱
s->next = p->next;  // 把p->next赋值给s的后继
p->next->prior = s;  // 把 s 赋值给p->next的前驱
p->next = s;    // 把s赋值给p的后继

删除

1
2
3
4


// 将结点 p 删除 
p->prior->next = p->next;  // 把p结点的前驱的后继指针 指向 p结点的后继
p->next->prior = p->prior;  // 把p结点的后继的前向指针 指向 p结点的前驱
free(p);

栈与队列

栈

栈(stack)：限定仅在表尾进行插入和删除操作的线性表。

一些名词解释：

栈顶(top)：允许插入和删除的一端
栈底(bottom)：与栈顶相反的一端。不含任何数据元素的栈称为空栈
进栈：栈的插入操作，也称为压栈、入栈
出栈：栈的删除操作，也称为弹栈

栈又称为 后进先出(Last In First Out) 的线性表，简称：LIFO结构。

注：进栈出栈的情况讨论。虽然说：栈对线性表的插入和删除后的位置进行了限制，但是并没有限制元素进出的时间。在所有元素还没完全都进栈的情况下，事先进去的元素也可以先出栈，只要保证栈顶元素出栈即可。

栈的抽象数据类型

ADT 栈(stack)

Data Description

同线性表。元素具有相同的类型，相邻元素具有前驱和后继关系。

Operation

InitStack(* S) ：初始化操作，建立一个空栈 S

DestroyStack(* S)：若栈存在，则销毁它

ClearStack(* S)：将栈清空

StackEmpty(S)：若栈为空，返回true；否则，返回false

GetTop(S, * e) ：若栈存在且非空，用e返回S的栈顶元素

Push(* S, e)：若栈存在，插入新元素e到栈S中并成为栈顶元素

Pop(* S, * e)：删除栈S中栈顶元素，并用e返回其值

StackLength(S)：返回栈S的元素个数

endADT

栈的顺序存储结构及实现

栈的顺序存储其实是线性表顺序存储的简化，称为顺序栈。

1
2
3
4
5
6


typedef int SElemType;  /* SElemType类型根据实际情况而定 */
/*顺序栈结构*/
typedef struct {
	SElemType data[MAXSIZE]; 
	int top;   // 栈顶指针
}SqStack;

进栈操作

1
2
3
4
5
6
7
8


/* 插入元素e 为新的栈顶元素 */
Status Push(SqStack *S, SElemType e) {
	if (S->top == MAXSIZE-1)  // 栈满，top指向数组下标末尾
		return ERROR;
	S->top++; // 栈指针加一
	S->data[S->top] = e; // 将新插入元素赋值给栈顶空间
	return OK;
}

出栈操作

1
2
3
4
5
6
7
8


// 若栈不为空，则删除S的栈顶元素，用e返回对应的值，并返回OK状态；否则返回ERROR
Status Pop(SqStack *S, SElemType *e) {
	if (S->top == -1) 
		return ERROR;
	*e = S->data[S->top]; // 先保存要删除的栈顶元素
	S->top--;
	return OK;
}

两栈共享空间

关键思路：顺序存储结构中，数组有两个端点，两个栈有两个栈底。

让其中一个栈的栈底为数组的始端，即：下标为0

另一个栈的栈底为数组的末端，即：下标为 n-1

这样两个栈若是增加元素，就是两端点向中间延伸

空间结构

1
2
3
4
5


typedef struct {
	SElemType data[MAXSIZE];
	int top1;   // 栈1栈顶指针
	int top2;   // 栈2栈顶指针
}SqDoubleStack;

进栈操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// 插入元素e 为新的栈顶元素
Status Push(SqDoubleStack *S, SElemType e, int stackNum) {
	if (S->top1+1 == S->top2)  // 栈已满
		return ERROR;
	if (stackNum == 1)   // 栈1有元素进栈
		S->data[++S->top1] = e;
	else if (stackNum == 2) 
		S->data[--S->top2] = e;
	return OK;
}

出栈操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


Status Pop(SqDoubleStack *S, SElemType *e, int stackNum) {
	if (stackNum == 1) {
		if (S->top1 == -1)
			return ERROR;
		*e = S->data[S->top1--];  // 栈1栈顶元素出栈
	} else if (stackNum == 2) {
		if (S->top2 == MAXSIZE) 
			return ERROR;
		*e = S->data[S->top2++];  // 栈2栈顶元素出栈
	}
	return OK;
}

使用场景：当两个栈的空间需求有相反关系时，可以使用这种数据结构。而且只是针对两个具有相同数据类型的栈的一个设计技巧。

栈的链式存储结构及实现

设计思路：将栈顶放在单链表的头部，即：把栈顶指针和单链表的头指针合二为一。故：对于链栈来说，不需要头结点了。

对于链栈来说，基本不存在栈满的情况。

1
2
3
4
5
6
7
8
9


typedef struct StackNode {
	SelemType data;
	struct StackNode *next;
}StackNode, *LinkStackPrt;

typedef struct {
	LinkStackPrt top;
	int count;
}LinkStack;

注：链栈的大部分操作和单链表类似，只是插入和删除上有所不同。

进栈操作

1
2
3
4
5
6
7
8


Status Push(LinkStack *S, SElemType e) {
	LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
	s->data = e;
	s->next = S->top;
	S->top = s;
	S->count++;
	return OK;
}

出栈操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


Status Pop(LinkStack *S, SElemType *e) {
	LinkStackPtr p;
	if (StackEmpty(*S))
		return ERROR;
	*e = S->top->data;
	p = S->top;
	S->top = S->top->next;
	free(p);
	S->count--;
	return OK;
}

不同存储方式栈结构的操作对比

顺序栈：
- 插入删除操作：时间复杂度O(1)
链式栈：
- 插入删除操作：时间复杂度O(1)

栈的作用

栈的引入，简化了程序设计的问题，划分了不同关注层次，使得思考范围缩小，更加聚焦于我们要解决的问题核心。

栈的应用——递归

把一个直接调用自己或通过一系列调用语句间接地调用自己的函数，称作：递归函数。

注：每个递归定义 必须至少有一个条件，满足时递归不再进行，不再引用自身而是直接返回。

编译器使用栈实现递归。

栈的应用(一)

1. 数制转换

例子如下：

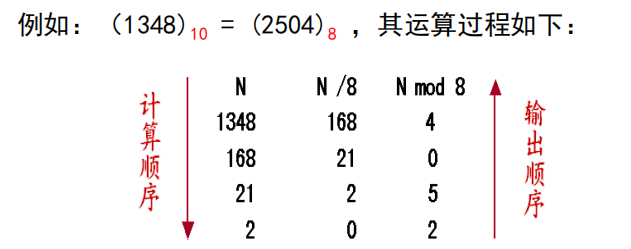
Pasted image 20231006205133

可以发现，上面的进制转换过程中，

计算时，从低位到高位顺序产生各个数位，即： N 取模后的数字
输出时，从高位到低位依次输出各个数位 倒序输出 “N 取模的数字”，这种顺序和栈特性LIFO 很匹配。故可以考虑用栈实现上述的进制转换算法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


// 实现函数：十进制数 转换为 八进制数
void conversion() {
	int num, val;
	SqStack s; // 创建新栈
	scanf("%d", num); // 读入一个十进制数
	while (num) {
		Push(&s, num % 8); // 余数 进栈
		num /= 8;   // 整除数
	}
	while (!Empty(&s)) {
		Pop(&s, &val);
		printf("%d", val);	
	}
	printf("\n");
}

2. 括号匹配校验

括号匹配算法描述：

初始化空栈，从左到右遍历表达式
读取第 i 个字符
- 若第 i 个字符是开始符号，则符号入栈
- 若第 i 个字符是结束符号
  - 栈空，匹配失败，退出
  - 栈不为空，取栈顶符号，检测是否是与结束符号相匹配的开始符号，若匹配，栈顶符号出栈；否则，匹配失败，退出
读取第 i+1 个字符
- 非末尾换行符，重复步骤2
- 已到达末尾换行符，若堆栈为空，匹配成功；否则，匹配失败

3. 迷宫求解

思路：DFS+回溯(使用栈来模拟递归)

栈的应用(二)——四则表达式求值

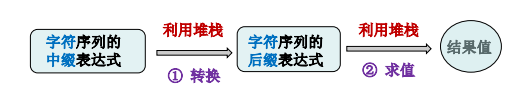
Pasted image 20231005173954

后缀(逆波兰)表示法

不同表达式表示法：

中缀表达式：运算符号位于两个运算数之间，如：a + b * c
后缀表达式：运算符号位于两个运算数之后，如：a b c * +

后缀表达式，也称为逆波兰(Reverse Polish Notation, RPN)，这种表达式可以不需要括号就反映出计算符号的优先顺序。

后缀表达式计算

运算规则：从左到右遍历表达式的每个数字和符号，遇到是数字(运算数)则进栈，遇到是符号(运算符)则将处于栈顶的两个数字出栈，进行运算，运算结果进栈。

重复前面过程，直到整个表达式遍历结束，栈顶元素即为表达式的值。

中缀表达式转后缀表达式

算法描述：从左到右遍历整个中缀表达式，对每个不同符号进行不同的区分操作：

空格：直接跳过
运算数：直接输出
左括号：压入栈中
右括号：括号中的中缀表达式扫描完毕，将栈顶运算符一次弹出，并输出，直到遇到左括号(左括号不输出)
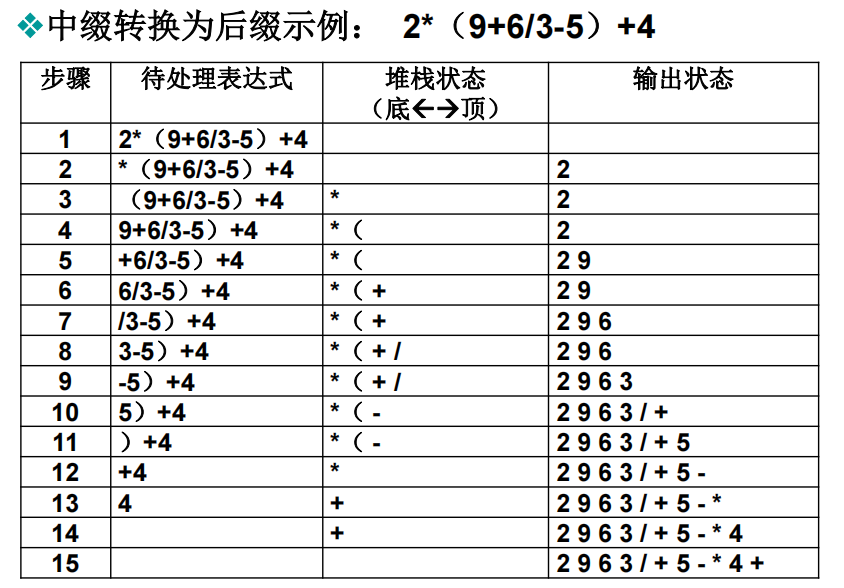
运算符：当前运算符 优先级 高于 栈顶运算符，则将当前运算符压入栈；当前运算符 优先级 不高于 栈顶运算符，则将 栈顶运算符弹出并输出(括号不输出)，接着继续比对栈顶运算符，重复前面操作

注：运算符这个入栈出栈规则，很类似单调栈的处理方式。

例子如下：

Pasted image 20231006203637

队列

队列(queue)：只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种 先进先出(First In First Out) 的线性表，简称FIFO。允许插入的一段称为队尾，允许删除的一端称为队头。

队列在程序中应用广泛。例如：键盘进行各种字母或数字的输入、显示器上如记事本软件上的输出等。

队列的抽象数据结构

ADT 队列(Queue)

Data

同线性表。元素具有相同的类型，相邻元素具有前驱和后继关系。

Operation

InitQueue(* Q)：初始化操作，建立一个空队列Q

DestroyQueue(* Q)：若队列Q存在，则销毁它

ClearQueue(* Q)：队列清空

QueueEmpty(Q)：若队列为空，返回true；否则，返回false

GetHead(Q, * e)：若队列存在且非空，用e返回队列Q 的队头元素

EnQueue(* Q, e)：若队列Q存在，插入新元素e到队列Q中并成为队尾元素

DeQueue(* Q, * e)：删除队列中队头元素，并用e返回其值

QueueLength(Q)：返回队列Q的元素个数

endADT

队列的顺序存储结构——循环队列设计

循环队列定义：队列头尾相接的顺序存储结构。

队头指针和队尾指针：

队头指针：始终指向队头元素
队尾指针：始终指向队列尾元素的下一个位置(非空顺序队列)

1
2
3
4
5
6
7
8


typedef int QElemType;  // QElemType 为元素类型
#define  MAXSIZE 100 
// 循环队列存储结构
typedef struct {
	QElemType data[MAXSIZE]; 
	int front;  // 头指针
	int rear;  // 尾指针，若队列不为空，指向队列尾部元素的 下一个位置
}SqQueue;

循环队列相关公式

通用计算队列长度的公式：(rear - front + QueueSize) % QueueSize
判断队满情况：(rear + 1) % QueueSize == front
判断队空情况：rear == front

初始化操作

1
2
3
4
5
6


// 初始化空队列
Status InitQueue(SqQueue *Q) {
	Q->front = 0;
	Q->rear = 0;
	return OK;
}

获取队列长度

1
2
3
4


// 返回Q 的元素个数，即 队列的当前长度
int QueueLength(SqQueue Q) {
	return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

循环队列入队操作

1
2
3
4
5
6
7
8
9


// 若队列未满，则插入元素 e 为Q的队尾元素
Status EnQueue(SqQueue *Q, QElemType e) {
	if ((Q->rear + 1) % MAXSIZE == Q->front)
		return ERROR;
	Q->data[Q->rear] = e;
	Q->rear = (Q->rear + 1) % MAXSIZE;

	return OK;
}

循环队列出队操作

1
2
3
4
5
6
7
8
9


// 若队列不为空，则删除队列Q中队头元素，用e返回其值
Status DeQueue(SqQueue *Q, QElemType *e) {
	if (Q->front == Q->rear)
		return ERROR;
	*e = Q->data[Q->front];
	Q->front = (Q->front+1) % MAXSIZE; 

	return OK;
}

时间复杂度分析

入队操作：O(1)
出队操作：O(1)

队列的链式存储结构及实现

队列的链式存储结构：线性表的单链表，限制队尾进队头出，简称为 链队列。

为了操作上的方便，将队头指针指向链队列的头结点，而队尾指针指向终端结点。

注意：头结点不存储数据。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


typedef int QElemType;  
typedef struct QNode {
	QElemType data;
	struct QNode *next;
}QNode, *QueuePtr;

// 队列的链表结构
typedef struct {
	QueuePtr front, rear;
}LinkQueue;

链队列初始化

1
2
3
4
5
6
7
8


Status InitQueue(LinkQueue *Q) {
	Q->front = (QueuePtr)malloc(sizeof(QNode));
	if (!Q->front) 
		exit(OVERFLOW);
	Q->rear = Q->front;  // 重要步骤
	Q->front->next = NULL;  // 重要步骤
	return OK;
}

链队列销毁

1
2
3
4
5
6
7


void DestoryQueue(LinkQueue *Q) {
	while (Q->front) {
		Q->rear = Q->front->next;
		free(Q->front);
		Q->front = Q->rear;
	}
}

入队操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


// 插入元素e 为新的队尾元素
Status EnQueue(LinkQueue *Q, QElemType e) {
	QueuePtr s = (QueuePtr)malloc(sizeof(QNode));
	if (!s) 
		exit(OVERFLOW);
	s->data = e;
	s->next = NULL;
	Q->rear->next = s;
	Q->rear = s;
	return OK;
}

出队操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


Status DeQueue(LinkQueue *Q, QElemType *e) {
	QueuePtr p;
	if (Q->front = Q->rear) 
		return ERROR;
	p = Q->front->next;
	*e = p->data;
	Q->front->next = p->next;
	if (Q->rear == p)   // 若队头就是队尾，则删除 后将 rear 指向头结点
		Q->rear = Q->front;
	free(p);
	return OK;
}

使用建议：在确定队列的长度最大值情况下，建议使用循环队列；若是无法预估队列的长度，则用链队列。

链队列和循环队列对比

链队列：无队列满问题，动态分配空间
循环队列：通过取模运算解决顺序队列的假溢出问题，只浪费1个空间

优先队列

串

串(string)：是由零个或者多个字符组成的有限序列(串的相邻字符之间具有前驱和后继关系)，又叫字符串。

一般记为 s = “a₁ a₂ … a_n " (n >= 0)，其中 s 是串的名称，双引号括起来的字符序列为串的值。

其中，字符数目n 为串的长度，i 为对应字符在串中的位置。

一些概念解释：

空串：零个字符的串
空格串：只包含空格的串。空格串是有长度的，而且可以不止一个字符。
子串和主串：串中 任意个数的连续字符组成的子序列称为该串的子串；相应的，包含子串的串称为主串。
位序：子串在主串中的位置，即：子串第一个字符在主串中的序号。
模式匹配：确定子串在主串中首次出现的位置的一种运算。

串的比较

串的比较是通过 组成串的字符之间的编码来进行的。

计算机中的编码：

ASCII编码：常用字符使用标准ASCII编码，由 8位二进制数表示一个字符，总共可以表示 2⁸ = 256个字符。

Unicode编码：为了表示成百上千种语言和文字，通常采用 16位二进制表示一个字符，总共可以表示 2¹⁶ 个字符，约6.5万多个字符。不过，为了和ASCII编码兼容，Unicode的前256个字符与ASCII码完全相同。

串相等：当且仅当两个串长度以及它们各个对应位置的字符都相等，这两个串才算相等。

判断串的大小

给定两个串：s = “a₁ a₂ … a_n “， t = “b₁ b₂ … b_m “，满足以下条件之一时，s < t。

n < m，且 a_i = b_i (i = 1, 2, …, n)
存在某个 k <= min(m, n)，使得 a_j = b_j (j = 1, 2, …, k-1)，a_k < b_k

串的抽象数据类型

ADT 串(string)

Data

串中元素仅由一个字符组成，相邻元素具有前驱和后继关系。

Operation

StrAssign(T, * chars) ：生成一个值等于字符串常量 chars的串T(C++string中，重载 = 运算符可以得到类似功能)

StrCopy(T, S)：串S存在，由串S复制得串T(C++string中，重载 = 运算符可以得到类似功能)

ClearString(S)：串S存在，将串清空

StringEmpty(S)：若串S为空，则返回true；否则，返回false

StrLength(S)：返回串S的元素个数，即：串的长度

StrCompare(S, T)：若S > T，返回值 > 0；若S = T，返回0；若S < T，返回值 < 0

Concat(T, S1, S2)：用T返回由S1和S2联接而成的新串

SubString(Sub, S, pos, len)：串S存在，1<= pos <= StrLength(S)，且0 <= len <= StrLength(S)-pos+1，用Sub 返回串S的第pos个字符起长度为len的子串

Index(S, T, pos)：串S和T存在，T是非空串，1<= pos <= StrLength(S)。返回主串S中第 pos 字符之后第一次出现和 T相同的子串的位置，若不存在，返回0

Replace(S, T, V)：串S、T和V存在，T是非空串。用V替换主串S中出现的所有与T相等的不重叠的子串

StrInsert(S, pos, T)：串S和T存在，1 <= pos <= StrLength(S)+1。在串S的第pos个字符之前插入串T

StrDelete(S, pos, len)：串S存在，1 <= pos <= StrLength(S)-len+1.从串S中删除第pos个字符起长度为len的子串。

endADT

注：串的抽象数据类型和线性表很像，不同之处：串针对的是字符集。线性表更关注 单个元素的指定操作，例如：查找一个元素，插入或删除一个元素；串中更多是 查找子串位置、得到指定位置子串、替换子串等操作。

操作Index算法实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


int Index(String S, String T, int pos) {
	int n, m, i;
	String Sub;
	if (pos > 0) {
		n = StrLength(S);   //  得到主串S的长度
		m = StrLength(T);   //  得到子串T的长度
		while(i <= n-m+1) {
			SubString(sub, S, i, m);   // 取主串中 第i个位置开始长度与T相等的子串 给sub
			if (StrCompare(sub, T) != 0) {
				++i;
			} else 
				return i;
		}
	}
	return 0;  // 若 无子串与T相等，返回0
}

串的存储结构

串的顺序存储结构

用一组地址连续的存储单元来存储串中的字符序列。

定长顺序存储表示

在C语言中，可以将串定义成 字符数组，利用串名可以直接访问串值。用这种表示方式，串的存储空间在编译时确定，大小不能改变。定义如下：

1
2


#define MAX_STRLEN 255
typedef unsigned char str[MAX_STRLEN+1];  // 第一个位置可以存储实际字符长度

定义了长度为 MAX_STRLEN的字符存储空间
字符串长度为不大于 MSX_STRLEN的任何值(串的最大长度限制，多余部分将被截断)

串的联接 Concat算法实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


Status Concat(String T, String S1, String S2) {
	int i;
	Status uncut;
	if (S1[0]+S2[0] <= MAX_STRLEN) { // S1 和 S2 均未截断
		for (i = 1; i <= S1[0]; i++) T[i] = S1[i];
		for (i = 1; i <= S2[0]; i++) T[i + S1[0]] = S2[i];
		T[0] = S1[0] + S2[0];
		uncut = true;
	} else if (S1[0] < MAX_STRLEN) {  // 截断 S2
		for (i = 1; i <= S1[0]; i++) T[i] = S1[i];
		for (i = S1[0]+1; i <= MAX_STRLEN; i++) T[i] = S2[i-S1[0]];
		T[0] = MAX_STRLEN;
		uncut = false;
	} else {   // 截断S1
		for (i = 0; i <= MAX_STRLEN; i++) T[i] = S1[i];
		uncut = false;
	}
	return uncut;
}

注意：定长数组表示的串，存在预定义的最大串长度MAX_STRLEN, 一般将实际的串长度存在数组下标为0位置，上面伪代码就是这样实现的。当然某些高级语言，例如：C语言，会规定在串的值后面加一个不计入串长度的结束标识符 \0，来表示串值终结。(故：StrLength一般都是通过遍历串计算的)

求子串 SubString算法实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


Status SubString(String Sub, String S, int pos, int len) {
	// 用Sub返回串S 的第pos个字符起长度为len的子串
	int i;
	if (pos < 1 || pos > S[0] || len < 0 || len > S[0]-pos+1)
		return ERROR;
	for (i = 1; i <= len; i++) 
		Sub[i] = S[pos+i-1];
	Sub[0] = len;
	return OK;
}

堆分配存储表示

串的存储空间仍然是连续的，且是程序运行时根据串的实际长度动态分配的。

C语言中，动态分配(malloc) 一组地址连续的存储单元，用于存储字符序列。

由malloc()和free()动态分配与回收 的存储空间称为堆。

堆分配串定义如下：

1
2
3
4


typedef struct {
	char *ch;   // 若非空，按照长度分配，否则为NULL
	int length;  // 串的长度
}HString;

堆分配的串插入：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


Status StrInsert(HString S, int pos, Hstring T) {
	// 1 <= pos <= StrLength(S)+1  在串S的第pos个字符之前插入串T
	int i;
	if (pos < 1 || pos > S.length+1) // pos不合法
		return ERROR;
	if (T.length) {   // T 非空，则重新分配空间，插入T
		if (!(S.ch = (char*)realloc(S.ch, (S.length+T.length+1)*sizeof(char) )))
			return ERROR;
		for (i = S.length-1; i >= pos-1; --i) {  // 为插入T 腾空间位置
			S.ch[i+T.length] = S.ch[i];
		for (i = 0; i < T.length; i++) // 插入T
			S.ch[pos-1+i] = T.ch[i];
		S.length += T.length;
		}
	}
	return OK;
} // StrInsert

串的链式存储结构

采用链表方式存储串值，每个结点中：

可以存放一个字符(结点大小为1)；
也可以存放n个字符(结点大小为n)。最后一个结点若是未被占满，可以用 “#“来补全，如下：

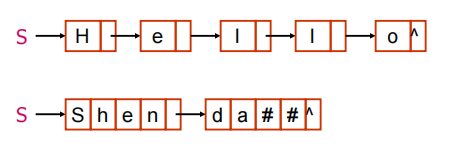
Pasted image 20231016040848

注：串的链式存储结构，除了在连接串与串操作时有一定的方便之外，总的来说不如顺序存储灵活，性能也不如顺序存储结构好。

块链存储的串定义如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


#define CHUNKSIZE 80
typedef struct Chunk {
	char ch[CHUNKSIZE];
	struct Chunk *next;
}Chunk;

typedef struct {
	Chunk *head, *tail; // 头尾指针
	int curLength;     // 当前长度
}LString;

块链存储密度

Pasted image 20231016042553

串的块链存储与单字符存储区别：

Pasted image 20231016042716

朴素的模式匹配算法

模式匹配：子串在主串中的定位操作。

模式匹配的应用在非常广泛。例如，在文本编辑程序中，我们经常要查找某一特定单词在文本中出现的位置。显然，解此问题的有效算法能极大地提高文本编辑程序的响应性能。

以下讨论定长顺序结构表示的串 的几种算法：

简单匹配算法/朴素匹配算法(BF(Brute-Force)算法)
KMP算法

朴素算法(BF算法)

采用穷举思想进行匹配：

从主串的指定位置开始，将主串与模式串(要查找的子串)的第一个字符比较;
若相等，则继续逐个比较后续字符;
若不等，从主串的下一个字符起再重新和模式串的第一个字符比较

伪代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


int Index(String S, String T, int pos) {
	// S 为主串，T为 模式串，串的第0位置存放串长度；串采用顺序存储结构
	i = pos; j = 1;
	while (i <= S[0] && j <= T[0]) {
		if (S[i] == T[j]) { ++i; ++j; }
		else { 
			i = i-j+2; // i 退回到上次匹配首位字符的下一位
			j = 1; // j 回退到模式串T的首位
		}
	}
	if (j > T[0])  return i-T[0];  // 返回与模式串 首字符相等的位置
	else return 0;  // 匹配失败
}

上面的算法中，主串指针i 回溯操作是算法操作的核心，即：i = i - j + 2;

性能分析

在第一个对齐位置只经过一轮比对之后，就能确定整体匹配，其时间复杂度为：O(m)（m为模式串的长度）
除匹配成功的位置外，其余位置仅需比较一次（模式串第一个字符），其时间复杂度为：O(n+m)(n，m分别为主串和模式串的长度)
匹配成功的最坏情况是，需要比较n-m+1趟，每趟比较m次，总比较次数达(n-m+1) * m，因此，其时间复杂度为O(n * m)

匹配成功最坏情况举例如下：

Pasted image 20231016050700

KMP模式匹配算法

由 D.E.Knuth、J.H.Morris和V.R.Pratt(其中Knuth和Pratt共同研究，Morris独立研究)发表一个模式匹配算法，可以大大避免重复遍历的清空，称之为克努特-莫里斯-普拉特算法，简称为KMP算法。

算法原理

利用模式串T 中隐藏的信息来提高模式匹配的效率。

KMP算法较BF算法有较大改进，主要消除了主串指针回退问题。

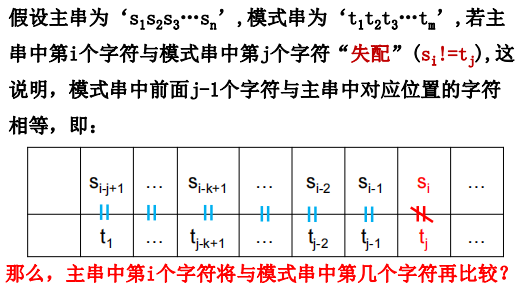
Pasted image 20231016213026

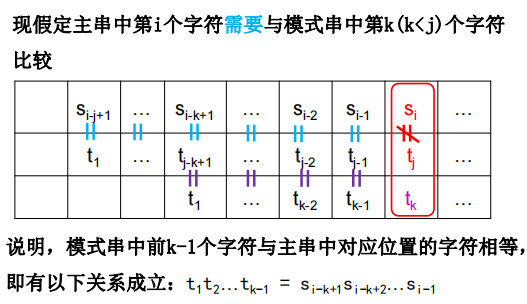
Pasted image 20231016213043

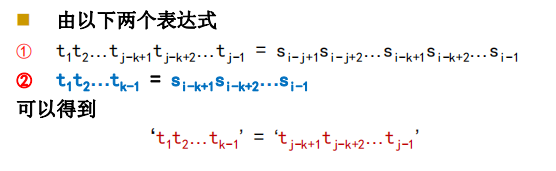
Pasted image 20231016213225

Pasted image 20231016213345

next数组值的推导

$$ next[j]=\left{ \begin{aligned} 0 & & \ 当j=1时 \ Max{k | 1 < k < j 且 ’t_{1}…t_{k-1}’ = ’t_{j-k+1}…t_{j-1}’}& & 当此集合非空时 \ 1 & & 其他情况 \end{aligned} \right. $$ Pasted image 20231016220941

算法实现

计算串的next数组

t[k] = t[j]情况：
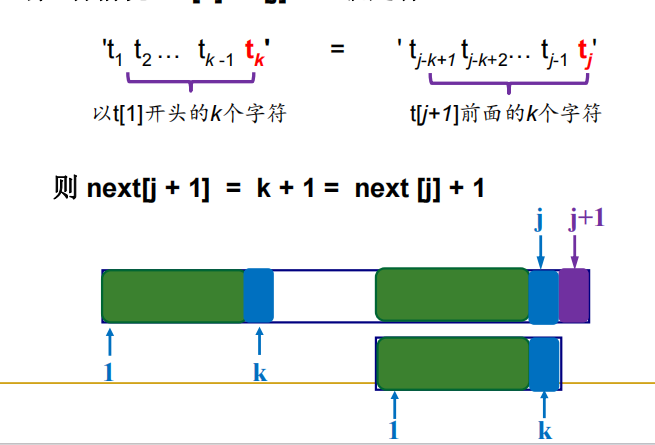
t[k] != t[j]情况，递归 k = next[k];

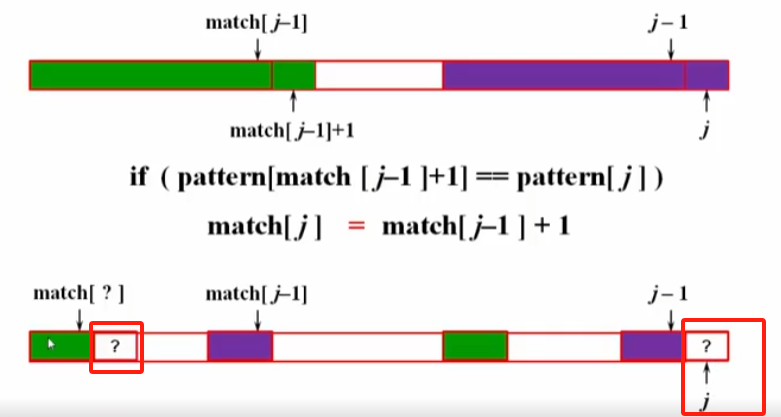
注意：上面的两张图中，图1是书上的next[j]定义，其含义为：

Pasted image 20231016220941

即：next[j] = k，这个k指向的是还未与 t_j 匹配的字符。故初始的 next[1] = 0;

图2是中国大学慕课上的浙大数据结构，其match[j] 的含义为：指向当前位置j之前，已经和 t_j-1 的匹配的相等的字符前缀的最后一个字符下标，如图中所示。故初始的 match[0]=-1;

基于对next数组定义的不同理解，以下给出两种不同构造next数组代码，KMP算法的实现参照第一种实现，即：next[1] = 0;的

初始化：next[1] = 0;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


void get_next(String T, int *next) {
	int i, k;
	i = 1;
	k = 0;
	next[1] = 0;  // 下面的T[0] 代表串的长度，串的有效值从 1开始到T[0]
	while (i < T[0]) {  // i = T[0]-1时，此时next[T[0]-1]已经计算完成，还可以进入循环计算next[T[0]]
		if (k == 0 || T[i] == T[k]) {
			++i;
			++k;
			next[i] = k;
		} else 
			k = next[k];     // 若字符不相同，则 k值回溯
	}
}

初始化：next[0] = -1;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// 求解长度为 len的字符串s 的next数组
void get_next(char s[], int len) {
	int j = -1;
	next[0] = -1;  // 初始化 j = next[0] = -1
	for (int i = 1; i < len; i++) {  // 求解 next[1]~next[len-1]
		j = next[i-1];
		while(j != -1 && s[i] != s[j+1]) { // 这里的 s[j]是 模式串相同前后缀 中 指向前缀最后一个后缀s[j]匹配的字符
			j = next[j];
		} // 直到 j回退到-1 或者 s[i] == s[j+1]
		/*if (s[i] == s[j+1])
			j++;  // 则 next[i] = j+1; 先令j指向这个位置 ，若是不匹配说明j == -1，不会进入判断，此时next[i] = -1
		next[i] = j; */
		// 代替上面被注释掉的代码，更加容易理解代码如下：
		if (s[i] == s[j+1])
			next[i] = j+1;
		else next[i] = -1;
	}
}

get_next函数时间复杂度分析：

上述get_next函数的第二种示例实现中，可以看到 for循环最多循环 m次(m为模式串的长度)，而 for循环的内部的while循环核心是j值的递归回溯，可以看到下面 next[i] = j+1;，即j值的递归回溯 次数不会超过 j值增加次数，而 j <= m，故综上：求next数组的时间复杂度为 O(m)。

next数组改进值 nextval数组

上面求next数组第一种方法中，若是 T[i] == T[k]会进行 ++i; ++k;的操作，而若是T[i] != T[k]，那会出现一种情况：若是 k位字符和它 next[k]指向的字符一致，那么会出现T[i] != T[next[k]]，要进一步回溯，找到 next[next[k]]然后再一次比对。

可以看出这是一种无效的计算，不如在计算 next值开始，若是出现 T[k] = T[next[k]]的情况，直接令：nextval[i] = nextval[k];，这样可以避免上面所说的无效计算。

改进之后的构造 nextval数组的函数如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


// 求 模式串T的next函数 修正值并存入 数组nextval
void get_nextval(String T, int *nextval) {
	int i, k;
	i = 1;
	k = 0;
	nextval[1] = 0;
	while (i < T[0]) {  // 此处T[0] 表示串T的长度
		if (k == 0 || T[i] == T[k]) {  // T[i] 表示后缀的单个字符，T[k]表示前缀的单个字符
			++i;
			++k;
			if (T[i] != T[k])  // 当前字符和前缀字符不同
				nextval[i] = k;  // 则 k为nextval在 i位置的值
			else 
				nextval[i] = nextval[k];   // 若是与前缀字符相同，则将前缀字符的
												// nextval值赋给 nextval在i位置的值
		} else 
			k = nextval[k];    // 若是字符不相同，则 k值回溯
	}
}

KMP算法实现

Pasted image 20231016222227

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


// 返回模式串 T 在 主串 S 中第pos个字符之后的位置。若不存在，则函数返回值为0
// T非空， 1<= pos <= StrLength(S)
int Index_KMP(String S, String T, int pos) {
	int i = pos;   // i 用于主串S中当前位置下标值，从pos开始匹配
	int j = 1;     // j 用于子串T中当前位置下标值
	int next[255];
	get_next(T, next);   // 对串 T做分析，得到其 next数组
	while (i <= S[0] && j <= T[0]) {  // 这里 字符串长度存在 字符数组的第一个位置
		if (j == 0 || S[i] = T[j]) {  // 两字母相等继续，比朴素算法增加了 j = 0判断
			++i; ++j;   
		} else {            // 指针后退重新开始匹配
			j = next[j];     // j 退回合适的位置，i值不变
		}
	}
	if (j > T[0]) 
		return i-T[0];
	else 
		return 0;
}

由于指向主串下标的i不回溯，while循环的时间复杂度为O(n)，而子串长度为m，只涉及到简单循环，时间复杂度为O(m)。故整个算法的时间复杂度为O(n+m)。(而 get_next操作的时间复杂度为 O(m) )

Pasted image 20231017022845

附录

参考文献

《大话数据结构》
《算法笔记》
《数据结构：思想与实现》
MOOC 数据结构-浙江大学

版权信息

本文原载于kitebin.top，遵循CC BY-NC-SA 4.0协议，复制请保留原文出处。

线性表

线性表的抽象数据类型

顺序表

线性表顺序存储结构代码

顺序存储结构的插入与删除

获得元素操作

插入操作

删除操作

顺序表类实现

DS顺序表—存储结构与操作

单链表

头指针与头结点异同

头指针

头结点

线性表链式存储结构代码

单链表的读取

单链表的插入与删除

单链表的插入

单链表的删除

单链表的整表创建

头插法

尾插法

单链表的整表删除

单链表结构与顺序存储结构优缺点

存储分配方式

时间性能

空间性能

单链表类实现

DS单链表–存储结构与操作

静态链表

静态链表存储结构

静态链表初始化

静态链表的插入操作

静态链表的删除操作

静态链表的优缺点

优点

缺点

小结

循环链表

循环链表与单链表差异

改造循环链表

头指针代表循环链表 或 尾指针代表循环链表 区别

尾指针代表循环链表 例子

双向链表

存储结构

双向链表中与单链表相同的操作

插入与删除操作

插入

删除

栈与队列

栈

栈的抽象数据类型

栈的顺序存储结构及实现

进栈操作

出栈操作

两栈共享空间

空间结构

进栈操作

出栈操作

栈的链式存储结构及实现

进栈操作

出栈操作

栈的作用

栈的应用——递归

栈的应用(一)

1. 数制转换

2. 括号匹配校验

3. 迷宫求解

栈的应用(二)——四则表达式求值

后缀(逆波兰)表示法

后缀表达式计算

中缀表达式转后缀表达式

队列

队列的抽象数据结构

队列的顺序存储结构——循环队列设计

循环队列相关公式

初始化操作

获取队列长度

循环队列入队操作

循环队列出队操作

头指针代表循环链表或尾指针代表循环链表区别

尾指针代表循环链表例子

定长顺序存储表示