树的定义与基础概念

树的定义

树(Tree)是n(n >= 0)个结点的有限集合。n = 0时称为空树。在任意一颗非空树中：

1. 有且仅有一个特定的称为 根(root)的结点
2. 当 n > 1时，其余结点可分为m(m > 0)个互不相交的有限集T₁ 、T₂ 、…、T_n ，其中每一个集合本身又是一颗树，并且称为 根的子树(SubTree)

从上面定义可以看出，树的定义除了第一点基础情况外，还包含着树的递归定义。这里强调几点：

• 树中包含树。每棵子树根节点有且仅有一个直接前驱，但可以有0个或多个后继
• 子树个数不限制，但它们一定是互不相交的。下面子树相交的例子则不符合树的定义：

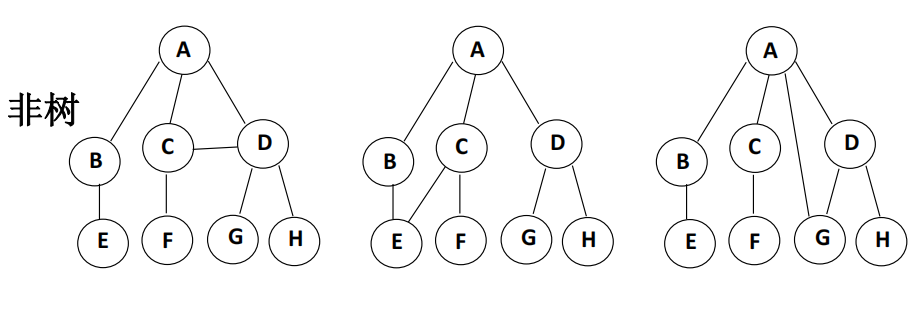
树的概念

结点分类

结点拥有的子树 数量称为 结点的度(Degree)。

• 度为0的结点称为 叶结点(Leaf)或 终端结点
• 度不为0结点，称为 分支结点 或 非终端结点
• 除根结点之外，分支结点也称为 内部结点。

注：树的度是树内各结点 度的最大值。

结点间的关系

1. 结点的子树的根，称为该结点的孩子(Child)；该结点称为 孩子的双亲(Parent)
2. 同一个双亲的孩子之间互称 兄弟(Sibling)
3. 结点的祖先：从根到该结点所经过 分支上所有结点；相反，以某结点为根的子树中的任一结点都称为 该结点的子孙
4. 树的层次：结点层次(Level)从根开始定义起，根为第一层，根的孩子为第二层
5. 某双亲在同一层的结点 互为 堂兄弟
6. 树中结点的最大层次称为 树的深度(Depth)或者高度
7. 若是将树中结点的各子树 看成从左到右是 有次序的，不能互换的，则称该树为有序树，否则称为无序树
8. 森林(Forest) 是 m (m>=0)棵互不相交的树的集合。对于树中每个结点而言，其子树 的集合即为森林。

树的抽象数据类型

ADT 树(tree)

Data

树是由一个根结点和若干棵子树构成的。树中结点具有相同数据类型以及层次关系。

Operation

• InitTree(* Tree)：构造空树T
• DestroyTree(* T)：销毁树T
• CreateTree(* T, definition)：按照definition中给出树的定义来构造树
• ClearTree(* T)：若树T存在，则将树T清为空树
• TreeEmpty(T)：若T为空树，返回true，否则返回false
• TreeDepth(T)：返回T的深度
• Root(T)：返回T的根结点
• Value(T, cur_e)：cur_e是树T中一个结点，返回此结点的值
• Assign(T, cur_e, value)：给树T的结点cur_e赋值为value
• Parent(T, cur_e)：若cur_e是树T的非根结点，则返回它的双亲；否则返回空
• LeftChild(T, cur_e)：若cur_e是树T的非叶结点，则返回它的最左孩子，否则返回空
• RightSibling(* T, * p, i, c)：其中p指向树T的某个结点，i所指结点p的度加上1，非空树c与T不相交，操作结果为插入c为 树T中p所指结点的第 i 棵子树
• DeleteChild(* T, * p, i)：其中p指向树T的某个结点，i为所指结点p的度，操作结果为删除T中p所指结点的第 i 棵子树

endADT

树的存储结构

树的某个结点的孩子可以有多个，这意味着，无论按何种顺序将树中所有结点存储到数组中，结点的存储位置都无法直接反映逻辑关系。简单的顺序存储结构是不能满足树的实现要求的。

充分利用顺序存储和链式存储结构的特点，完全可以实现对树的存储结构的表示。下面介绍三种不同的表示法：双亲表示法、孩子表示法、孩子兄弟表示法。

双亲表示法

示例如下：

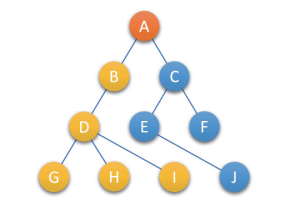
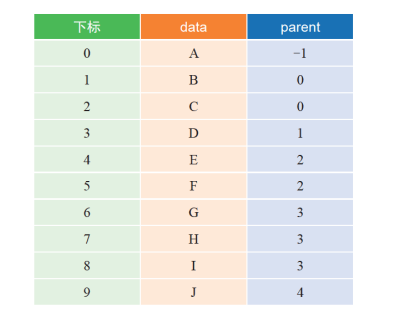
双亲表示法数据结构如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

#define MAX_TREE_SIZE 100

typedef int TElemType;   // 树结点的数据类型

typedef struct PTNode {  
	TElemType data;    // 结点数据
	int parent;        // 双亲位置
} PTNode;

typedef struct {
	PTNode nodes[MAX_TREE_SIZE];  // 结点数组
	int r, n;    // 根的位置 和 结点数
}PTree;

注：由于根结点没有双亲，约定根结点的位置域设置为 -1。这样可以根据parent指针很容易找到它的双亲结点，所用的时间复杂度为O(1)，直到parent为-1，表示找到了树的根。

不过如果要知道结点的孩子是谁，需要遍历整棵树。

如果结点孩子很多，超过2各。既关注 结点的双亲、又关注结点的孩子、还关注结点的兄弟，而且对时间遍历要求比较高，可以把上面数据结构拓展一下：包含 双亲域、长子域和右兄弟域，如下：

1
2
3
4

typedef struct PTNode {
	TElemType data;   // 结点数据
	int parent, firstchild, rightsib; // 双亲位置、长子位置以及 右兄弟位置
}PTNode;

注：一个存储结构设计是否合理，取决于 基于该存储结构的运算是否适合、是否方便，时间复杂度好不好等

孩子表示法

每个结点有多个指针域，其中每个指针指向一棵子树的根结点，我们把这种方法 叫做 多重链表表示法。

树中每个结点的度，也就是它的孩子个数是不同的，故有不同设计方案：

• 方案一：指针域个数 等于树的度数。若是不同结点度相差很大，显然很浪费空间。

注：树的度是树各个结点 度的最大值。

• 方案二：每个结点指针域的个数 等于该结点的度，专门取一个位置来存储结点指针域个数。这种方法克服了浪费空间的 缺点，对空间利用率提高了，但是由于各个结点的链表不同结构，加上要维护结点的度的数值，运算上会带来时间上的损耗。

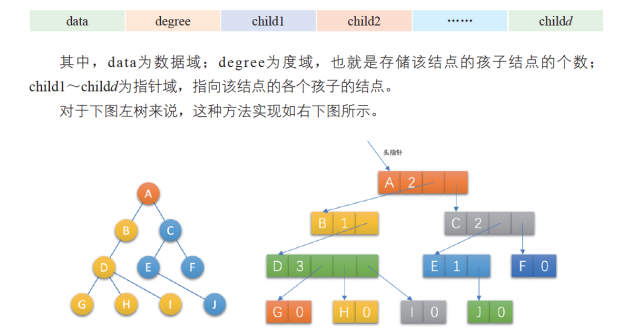
解决上面的问题，提出：孩子表示法：

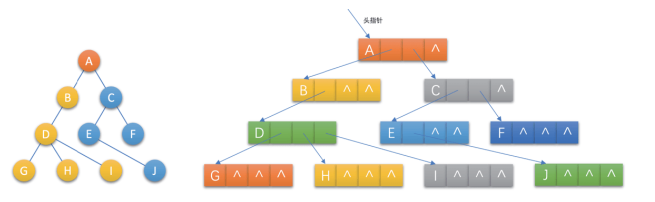
把每个结点的孩子结点排列起来，以单链表作为存储结构，则n个结点有n条链表，如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中。

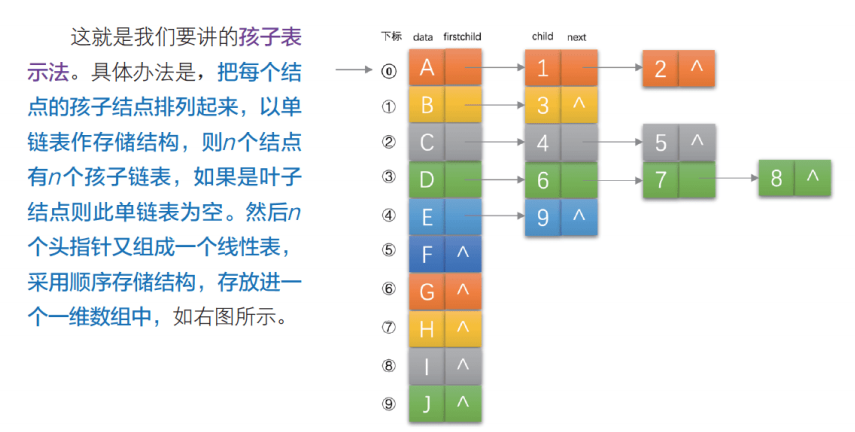
孩子表示法数据结构如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

#define MAX_TREE_SIZE 100  // 树的孩子表示法结构定义

typedef int TElemType;   // 树结点类型

typedef struct CTNode {
	int child;
	struct CTNode *next;
} *ChildPtr;

typedef struct {       // 表头结构
	TElemType data; 
	ChildPtr firstchild;
} CTBox;

typedef struct {   // 树结构
	CTBox nodes[MAX_TREE_SIZE];  // 结点数组
	int r, n;    // 根的位置和结点数
}CTree;

上述结构：对于查找某个结点的某个孩子，或者找某个结点的兄弟，只需要查找这个结点的孩子单链表。

遍历整颗树，只需要对头结点数组进行循环遍历即可

不过，存在问题：如何知道某个结点的双亲是谁呢？答：需要整颗树遍历。

优化，把双亲表示法和孩子表示法综合一下，如下：

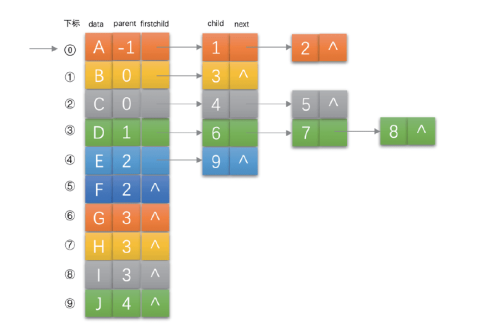
双亲孩子表示法 数据结构如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

#define MAX_TREE_SIZE 100  // 树的孩子表示法结构定义

typedef int TElemType;   // 树结点类型

typedef struct CTNode {
	int child;
	struct CTNode *next;
} *ChildPtr;

typedef struct {       // 表头结构
	TElemType data; 
	ChildPtr firstchild;
	int parent;  // 在结点数组 结构中添加 双亲结点下标
} CTBox;

typedef struct {   // 树结构
	CTBox nodes[MAX_TREE_SIZE];  // 结点数组
	int r, n;    // 根的位置和结点数
}CTree;

上述表示方法 称为 双亲孩子表示法。算是孩子表示法的改进。

孩子兄弟表示法

任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。故可以设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟

1
2
3
4
5
6

// 树的 孩子兄弟表示法 结构定义
// CSNode : child sibling Node
typedef struct CSNode {
	TElemType data;
	struct CSNode *firstchild, *rightsib;
} CSNode, *CSTree;

示例如下：

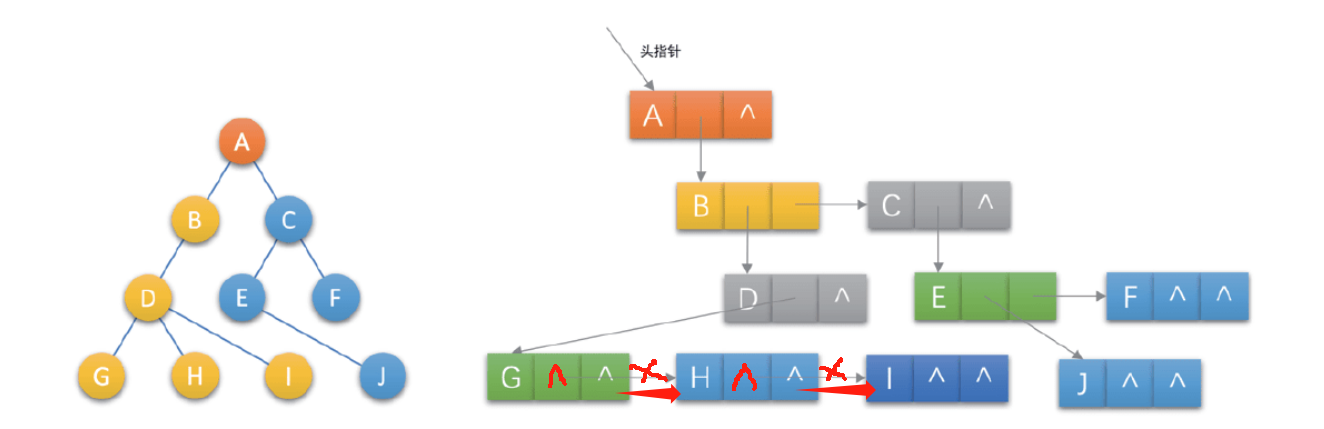
这种表示法，给查找某个结点的某个孩子带来了方便，只需要通过 firstchilde即可找到结点的长子，再通过长子结点的rightsib找到其兄弟。

若是需要找到某个结点的双亲，可以添加一个parent指针。

孩子兄弟表示法好处：把一颗复杂的树变成一棵二叉树。 把上面图形变化一下，如下图：

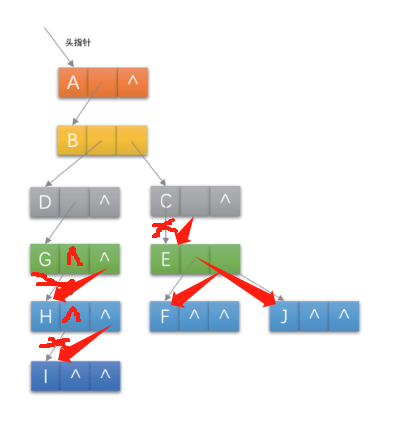
这样就可以 利用二叉树的特性和算法来处理这颗树了。

二叉树

对于 在某个阶段都是两种结果的情形，比如：开和关、0和1、真和假、上和下、正面与反面等，都适用树状结构来建模，而这种树是一种很特殊的树状结构，即：二叉树。

二叉树(Binary Tree)是n (n >= 0) 个结点的有限集合，该集合或者为空集(空二叉树)，或者由一个根结点和两棵互不相交的、分别称为根结点的 左子树和右子树的二叉树组成。

二叉树特点

• 每个结点 最多有两棵子树。故二叉树中不存在度大于2的结点(出度)
• 左子树和右子树是有顺序的
• 树中某结点 只有一棵子树，也要区分它是左子树还是右子树。

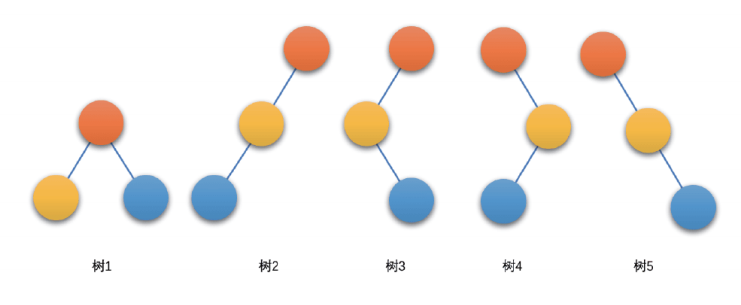
二叉树五种基本形态如下：

三个结点的树的五种形态如下：

特殊二叉树

斜树

所有结点只有左子树的二叉树叫作 左斜树；所有结点只有右子树的二叉树叫作 右斜树。二者统称为 斜树。

斜树特点：每一层只有一个结点，结点的个数与二叉树的深度相同。和线性表等同。所以，线性表也可以理解为树的一种特俗表现形式。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为 满二叉树。

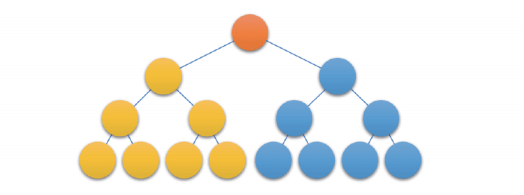
满二叉树特点：

• 叶子只能出现在最下一层
• 非叶子结点的度一定为2
• 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多

完全二叉树

对一棵具有n个结点的二叉树 按层序编号，如果编号为i(1 <= i <= n)的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

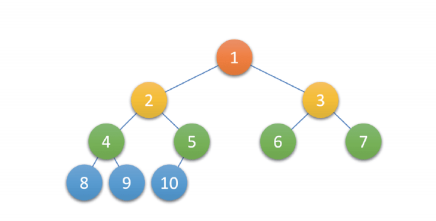
完全二叉树特点：

• 叶子结点只能出现在 最下两层
• 最下层的叶子一定集中在左部连续位置
• 倒数第二层，若有叶子结点，一定都在右部连续位置
• 如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况
• 同样结点数的二叉树，完全二叉树的深度最小

二叉树性质

性质1

在二叉树的 第i层 至多有 2^i-1 结点(i >= 1)

性质2

深度为k 的二叉树至多有 2^k - 1个结点 (k >= 1)

性质3

对任何一棵二叉树T，如果其终端结点数为n₀，度为2的结点数为n₂ ，则n₂ + 1 = n₀

推导：假设n₁ 为度是1的结点数，则树T结点总数为：n = n₀ + n₁ + n₂ ，树的分支数量为：2n₂ + n₁，又 n - 1 = 2n₂ + n₁ ， 故得出结论：n₂ + 1 = n₀

性质4

具有n 个结点的完全二叉树的深度为 [log₂ n] + 1 ([x] 表示不大于x的最大整数)

推导：设完全二叉树结点数为n，则n一定小于等于同样深度的满二叉树结点数 2^k -1，一定多于 2^k-1 -1， 即满足：2^k-1 - 1 < n <= 2^k -1。对不等式两边取对数，得：k - 1 <= log₂ n < k，k作为深度为整数，故：k = $[log_2 n]$ + 1。

性质5

如果对一棵有 n 个结点的完全二叉树的结点进行编号(从第1层到第$[log_2n]$ + 1层，每层从左到右)，对任一结点i(1 <= i <= n)有：

• 如果i = 1， 则结点i是二叉树的根，无双亲；如果i > 1， 则其双亲是结点i / 2
• 如果 2i > n， 则结点i无左孩子(结点i为叶子结点)；否则其左孩子是结点2i
• 如果 2i+1 > n， 则结点i无右孩子；否则其右孩子的结点为2i+1

二叉树的存储结构

顺序存储结构

用一维数组存储二叉树中的结点，并且结点的存储位置(数组下标)要体现 结点之间的逻辑关系，例如：双亲和孩子的关系，左右兄弟的关系等

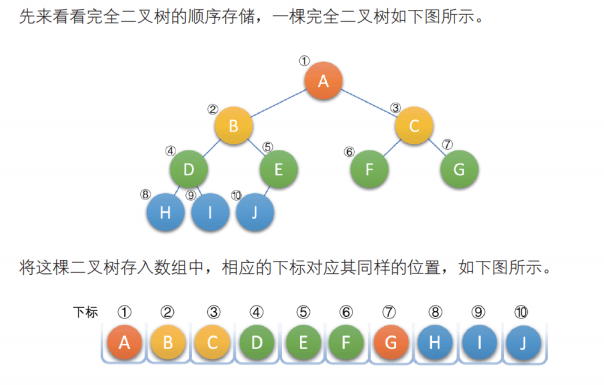
一般二叉树，也可以按照完全二叉树编号，把不存在的结点设置为 ‘^‘即可，如下：

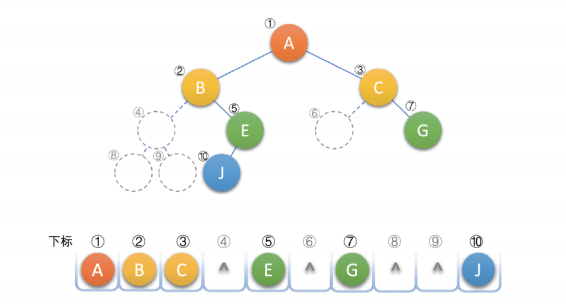
注：顺序存储结构一般用于存储完全二叉树。

二叉链表

二叉树结点最多有两个孩子,设计 一个数据域和两个指针域的结构是比较自然的想法,称这种链表为 二叉链表.

1
2
3
4
5

// 二叉树的二叉链表结点结构
typedef struct BiTNode {
	TElemType data;  // 结点数据
	struct BiTNode *leftChild, rightChild; // 左右孩子指针
}BiTNode, *BiTree;

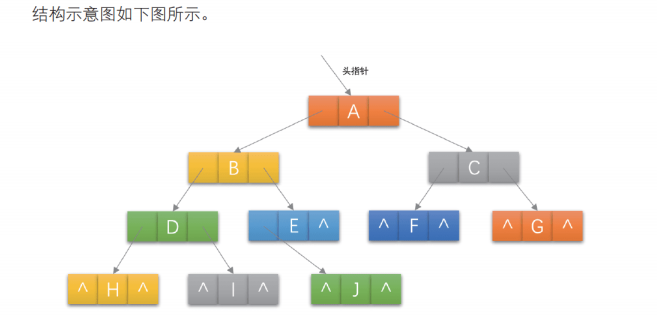
注:如果有需要,还可以增加一个 指向双亲的指针域, 这样的链表结构称为 三叉链表.

遍历二叉树

1. 遍历原理

二叉树遍历(traversing binary tree)是指从根结点出发,按照一定的次序依次访问二叉树中的所有结点,使得每个结点被访问一次且仅被访问一次.

两个关键的步骤: 访问 和 次序

• 访问:根据实际需要 来确定具体做什么, 例如:对每个结点进行相关计算或者打印等,算作是一个抽象操作.
• 次序: 二叉树遍历次序不同于线性结构, 线性结构无非是循环/双向等简单遍历方式. 树结点之间不存在 唯一的前驱和后继关系,在访问一个结点后,下一个访问的结点面临不同的选择

2. 遍历方法

1. 前序遍历: 若二叉树为空,则空操作返回 ; 否则, 先访问根结点,然后前序遍历左子树,在前序遍历右子树. 如下所示:
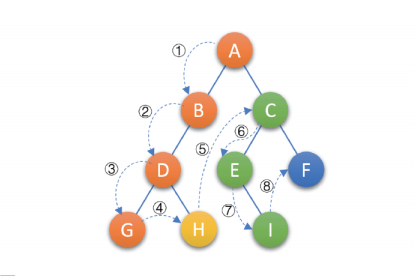
2. 中序遍历 : 若树为空,则空操作返回 ; 否则, 从根结点开始, 中序遍历根结点的左子树,然后访问 根结点, 接着中序遍历右子树. 如下图所示:
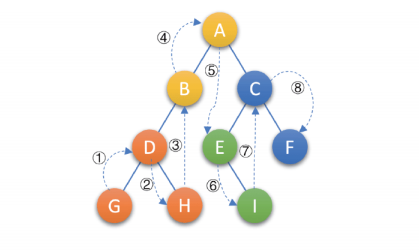
3. 后序遍历 : 若树为空,则空操作返回 ; 否则, 从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点，如下图所示：
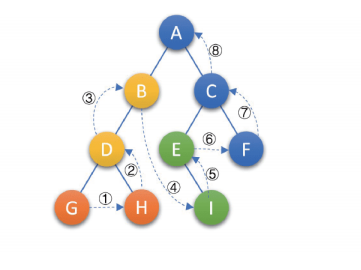
4. 层次遍历：若树为空，则空操作返回；否则，从树的第一层，即根结点开始访问，从上而下逐层遍历，在同一层中，按照从左到右的顺序对结点逐个访问，如下图所示：

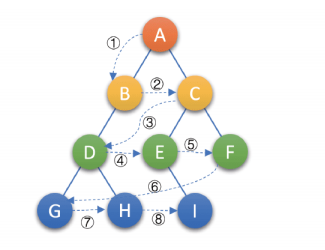
上述四种遍历方法，其实都是把树中的结点变成某种意义上的线性序列，这给程序的实现带来了好处。

此外，不同的遍历方式提供了对结点 进行不同次序的处理方式，可以在遍历过程中对结点进行各种处理。

3. 前序遍历算法

采用递归方式实现，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 二叉树的前序遍历递归算法
// 初始条件：二叉树T 存在
// 操作结果：前序遍历 T
void PreOrderTraverse(BiTree T) {
	if (T == NULL)
		return;
	printf("%c", T->data);  // 对结点操作，这里打印输出
	PreOrderTraverse(T->leftChild);
	PreOrderTraverse(T->rightChild);
}

4. 中序遍历算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 二叉树的中序遍历递归算法
// 初始条件：二叉树T 存在
// 操作结果：中序递归遍历 T
void InOrderTraverse(BiTree T) {
	if (T == NULL)
		return;
	InOrderTraverse(T->leftChild); // 中序遍历左子树
	printf("%c", T->data);  // 对结点操作，这里打印输出
	InOrderTraverse(T->rightChild); // 中序遍历右子树
}

5. 后序遍历算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 二叉树的后续遍历递归算法
// 初始条件：二叉树T存在
// 操作结果：后续递归遍历T
void PostOrderTraverse(BiTree T) {
	if (T == NULL) 
		return;
	PostOrderTraverse(T->leftChild); // 后续遍历左子树
	PostOrderTraverse(T->rightChild); // 后序遍历右子树
	printf("%c", T->data);  // 对结点操作，这里打印输出
}

6. 推导遍历结果

两个二叉树遍历的性质：

• 已知前序遍历序列和中序遍历序列，可以唯一确定一棵 二叉树
• 已知后序遍历序列和中序遍历序列，可以唯一确定一棵 二叉树

注意：已知前序和后续遍历，是不能唯一确定一棵二叉树的。如下：

前序序列为ABC，后序序列为CBA，可以确定A一定是根结点，但是无法确定：B和C哪个是左子树，哪个是右子树，这棵树形态有下面四种可能，如下：

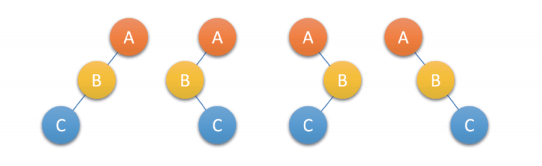
7. 树的遍历小结

遍历二叉树是 树算法中最基础也是最重要的需要牢牢掌握的基本功。前序、中序、后序以及层序遍历都是需要熟练掌握的。要学会用计算机的运行思维 去模拟递归的实现，考虑使用栈非递归实现上述的递归遍历算法，可以加深对递归的理解。

二叉树的建立

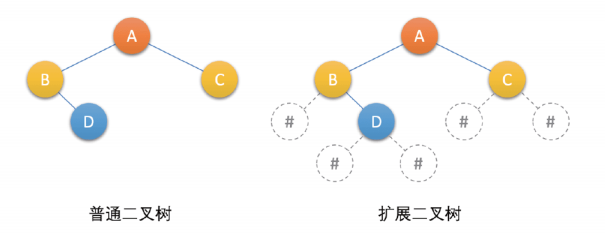
将普通二叉树中每个结点的空指针引出一个虚结点，其值为以特定值，例如“#”。将这种处理后的二叉树 称为 原二叉树的拓展二叉树。拓展二叉树可以做到一个遍历序列确定一棵二叉树，例如下面二叉树的前序遍历序列为：AB#D##C##，如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

// 按照 前序遍历输入二叉树中结点的值 (字符)
// 表示空树，构造二叉链表表示二叉树 T
// 本身 BiTree是BiTNode结点指针，而 BiTree* 则为指向BiTNode结点的二级指针
void CreateBiTree(BiTree *T) {
	TElemType ch;

	scanf("%c", &ch);  // 键盘输入
	//ch = str[index++];  // 直接字符串读入
	if (ch == '#') 
		*T = NULL;
	else {
		*T = (BiTree)malloc(sizeof(BiTNode));
		if (! *T) 
			exit(OVERFLOW);
		(*T)->data = ch;  // 生成根结点
		CreateBiTree(&((*T)->leftChild)); // 构造左子树
		CreateBiTree(&((*T)->rightChild));  // 构造右子树
	}
}

建立二叉树和 对应的遍历算法类似，将遍历算法中结点操作修改成生成结点、给结点赋值操作 即可。

线索二叉树

指向前驱和后继的指针称为 线索，加上线索的二叉链表称为 线索链表，相应的二叉树称为 线索二叉树(Threaded Binary Tree)。

思考一个问题：二叉树中空余的指针域能够将整棵二叉树中的结点通过 线索 串联起来么？

对于n个结点的二叉链表，每个结点有指向左右孩子的两个指针域，所以一共有 2n 个指针域。而 n个结点的二叉树一共有 n - 1条分支线数。也就是说，存在 2n - (n - 1) = n+1 个 空指针域。故这些指针域完全足以通过 线索 将所有结点串联起来！

线索化：对二叉树 以某种次序遍历使其变为线索二叉树的过程称作 线索化。

问题2：如何知道某一结点的 leftChild是指向它的左孩子还是指向前驱？rightChild是指向右孩子还是指向后继？

答：添加一个区分标志 tag。为每个结点增设两个标志域 ltag和rtag，应该注意 ltag和rtag只是存放0 或 1 数字的布尔型变量，其占用内存远小于leftChild和rightChild的指针变量，结构如下：

对于 左下图二叉链表图修改为 右下图：

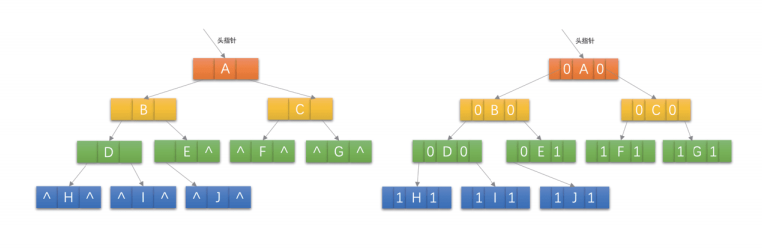
线索二叉树结构实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 二叉树的 二叉线索存储结构定义
typedef char TElemType;
typedef enum {Link, Thread} PointerTag;  // Link==0，表示指向左右孩子指针

typedef struct BiThrNode {    // 二叉线索 存储结构结构
	TElemType data;   // 结点数据
	struct BiThrNode *lchild, *rchild;  // 左右孩子指针
	PointerTag LTag;
	PointerTag RTag;     // 左右标志
} BiThrNode, *BiThrTree;

线索化的实质：将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱或者后继的信息只有在遍历该二叉树时才能得到。故：线索化的过程就是在遍历的过程中修改空指针的过程。

中序遍历线索化的递归函数代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

BiThrTree pre;   // 全局变量，始终指向刚刚访问过的结点
// 中序遍历 进行 中序线索化
void InThreading(BiThrTree p) {
	if (p) {
		InThreading(p->lchild);  // 递归左子树线索化
		
		if (! p->lchild) {
			p->LTag = Thread;  // 前驱线索
			p->lchild = pre;   // 左孩子指针 指向前驱
		} 
		if (! pre->rchild) {
			pre->TTag = Thread;  // 后继线索
			pre->rchild = p;   // 前驱的右孩子 指针指向后继(当前指针p)
		}
		pre = p;
		
		InThreading(p->rchild);  // 递归右子树 线索化
	}
}

可以发现，上面代码中间部分和二叉树中序遍历 中操作结点有较大差异外，其他操作和 二叉树中序遍历递归代码几乎一样。(只是将打印结点的功能改为线索化的功能了)

遍历线索二叉树

有了线索二叉树后，可以对它进行遍历，其实等于 操作一个双向链表结构。

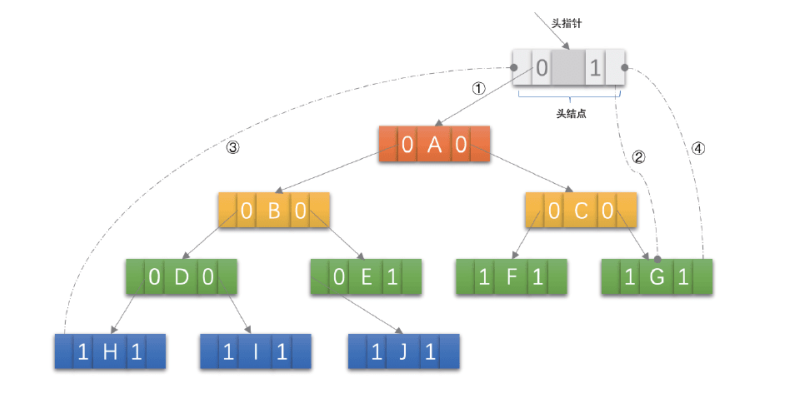
在二叉树线索链表上 添加一个头结点，如下图，令其 lchild域的指针指向二叉树的根结点(图中1)，其rchild域的指针指向中序遍历时访问的最后一个结点(图中2)。

反之，令二叉树的中序序列中的第一个结点中lchild域指针 和 最后一个结点的rchild域指针均指向头结点(图中3和4).

上面定义的好处：既可以从第一个结点起 顺后继进行遍历， 也可以从最后一个结点起 顺前驱进行遍历。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// T指向 头结点，头结点左指针 lchild指向根结点，头结点右指针 rchild指向中序遍历最后一个结点
// 中序遍历二叉线索链表 表示的二叉树T
Status InOrderTraverse_Thr(BiThrTree T) {
	BiThrTree p;
	p = T->lchild;   // p指向根结点
	while (p != T) {
		while (p->LTag == Link)  // 随着 LTag = 0 循环到中序序列的第一个结点
			p = p->lchild;
		printf("%c", p->data);   // 对结点进行操作
		while (p->RTag == Thread && p->rchild != T) {
			p = p->rchild;
			printf("%c", p->data);   // 访问后继结点
		}
		p = p->rchild;    // p 进到其 右子树的根
	}
	return OK;
}

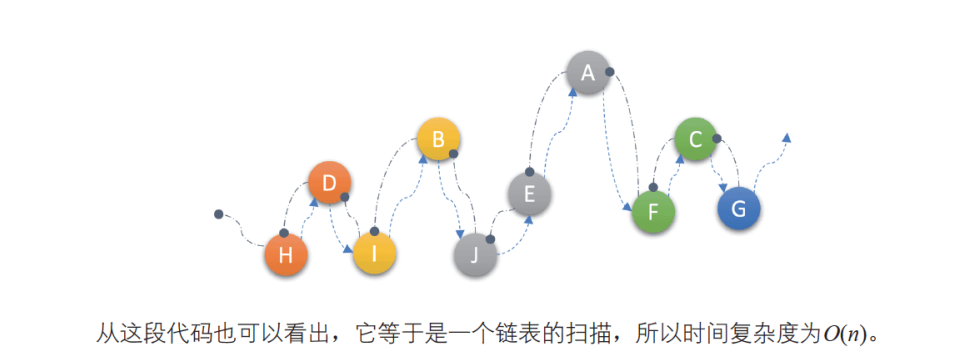
上面的遍历有点类似于中序遍历的思想，先p = p->lchild访问左子树，接着在while循环中通过链表指针中序遍历结点，最后p = p->rchild访问当前结点的 右子树。访问顺序还是：左子树->当前结点->右子树，符合中序遍历的顺序。

优点：

• 节约空间角度：充分利用了空指针域
• 节约时间角度：创建时，一次遍历就保存了前驱后继信息(将二叉树改造成 线索二叉链表)，可以重复使用

小结：实际问题中，如果所用的二叉树 需要经常遍历或者查找结点时，需要某种遍历序列中的前驱和后继，采用线索二叉链表的存储结构是不错的选择。

树、森林与二叉树的转换

在讲树的存储时，提到了树的孩子兄弟法，可以将一棵树用二叉链表进行存储，所以借助二叉链表，树和二叉树之间可以相互进行转换。

从物理结构来看，二叉链表都是相同的，只是含义不太一样。所以，只要设定一定的规则，用二叉树来表示树，甚至表示深林都是可以的。

树转换为二叉树

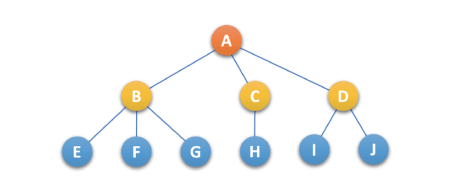
将上述的树 转化为 二叉树，步骤如下：

1. 加线：在所有兄弟结点之间 加一条连线，如下：
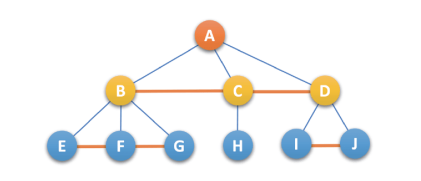
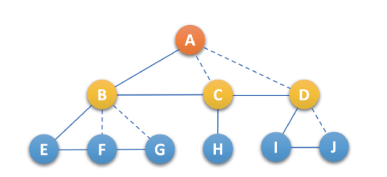
2. 去线：对树中每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线，如下：
3. 调整层次：以 树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明(树第一个孩子—> 二叉树中的左孩子，树的兄弟结点—> 二叉树中的右孩子)，如下图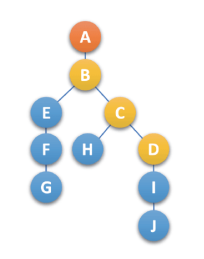： 注：结点F为结点E的兄弟，转换为结点E的右孩子；结点G为结点F的兄弟，转换为结点F的右孩子。

森林转化为二叉树

森林由若干棵树组成的，可以理解为：森林中的每一棵树都是兄弟，可以按照兄弟的处理方法来操作。

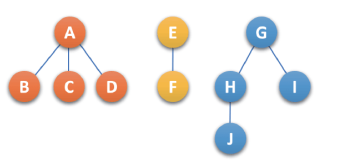
将上述森林的三棵树 转化为 一棵二叉树，步骤如下：

1. 把每棵树转化为二叉树，如下：
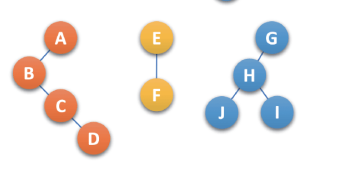
2. 第一颗二叉树不动，从第二棵二叉树开始，依次把后一颗二叉树的根结点 作为前一棵二叉树的右孩子，用线依次连接起来，如下：

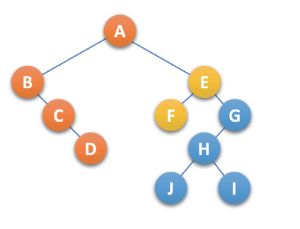
二叉树 转换为 树

二叉树转换为 树 是 树转换为二叉树的逆过程。例子如下：

将上述树转换为二叉树，步骤如下：

1. 加线：若某个结点的左孩子存在，则将结点 与 左孩子的右孩子(及其递归的右孩子)连线，如下：
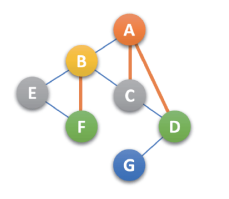
2. 去线：删除原二叉树中所有结点与其 右孩子结点的连线，如下：
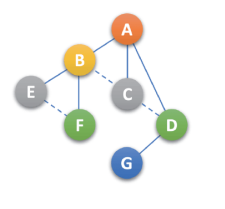
3. 调整层次

二叉树 转换为 森林

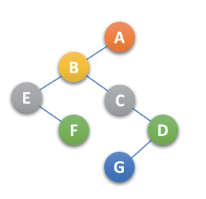
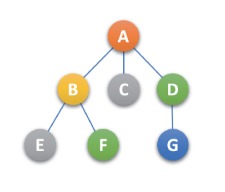
判断一棵二叉树 能否转换成 一棵树还是森林，有个关键：这课二叉树的根结点有没有右孩子，有就是森林，没有就是一棵树，例如下面例子就是可以转化为森林的二叉树，如下：

将上述二叉树转化为森林，步骤如下：

1. 从根结点开始，若右孩子存在，则把与右孩子结点的连线删除，如下图：
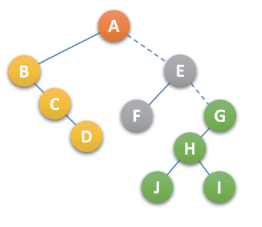
2. 再查看分离后的二叉树，根结点开始右孩子是否存在，若存在重复步骤1，知道所有右孩子连线都删除，得到彻底分离的二叉树，如下：
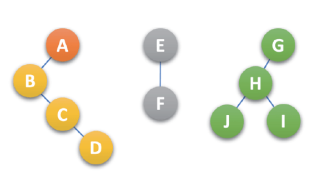
3. 将每棵分离后的二叉树转换为 树，如下：

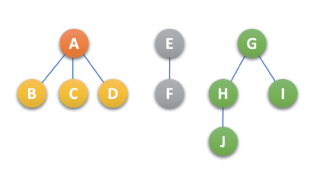
树与森林的遍历

树的遍历方式

• 先根遍历树：先访问树的根结点，然后依次先根遍历其 每一棵子树
• 后根遍历树：先依次 后根遍历每棵子树，然后访问根结点。

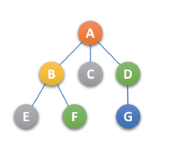
上述的树，先根遍历序列为：ABEFCDG，后根遍历序列为：EFBCGDA

森林的遍历方式

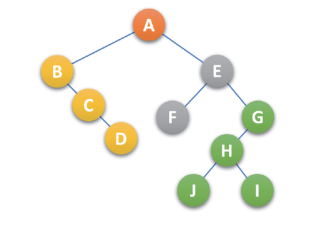
• 前序遍历：先访问森林中 第一棵树的根结点，然后再依次先根遍历根的每棵子树，再依次用同样的方式遍历除去第一棵树的剩余数构成的森林

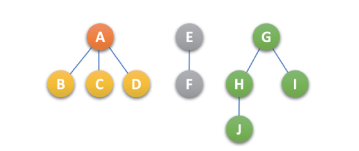
上述森林，前序遍历序列结果为：ABCDEFGHJI

• 后序遍历：先访问森林中 第一棵树，后根遍历的方式遍历每棵子树，然后再访问根结点，再依次用同样的方式遍历除去第一棵树的剩余树构成的森林

上述森林，后续遍历序列结果为：BCDAFEJHIG

对比分析

对下图二叉树进行分析，可以发现：森林的前序遍历和二叉树的 前序遍历结果相同，森林的后序遍历和二叉树的中序遍历结果相同。

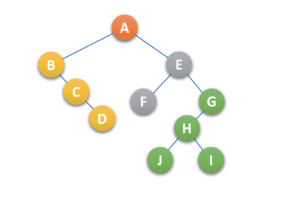
启示

当用 二叉链表 当作树的存储结构时，树的先根遍历和后根遍历 完全可以借用 二叉树的前序遍历和中序遍历的算法来实现。把树和森林 这种较为复杂结构树的遍历 通过转化为 二叉树的简单遍历算法实现。

赫夫曼树及其应用

美国数学家赫夫曼(David Huffman)，在1952年发明了赫夫曼编码，为了纪念他的成就，于是就把他在编码中用到的特殊二叉树称为赫夫曼树，其编码方法称为 赫夫曼编码(一种最基本的压缩编码方法)。

赫夫曼树的定义与原理

一些概念：

• 路径长度：从树中 一个结点 到 另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目 称做 路径长度。
• 树的路径长度：从树根 到每一个结点 的路径长度之和
• 带权路径长度：某一个结点 到树根之间的路径长度 与 结点上权值乘积
• 树的带权路径长度：树中 所有叶子结点 的带权路径长度之和

假设有n个权值 {w₁ , w₂ , … , w_n }，构造一棵有n个叶子结点的二叉树，每个叶子结点带权 w_i ，每个叶子结点的路径长度为 l_i ，则其中 带权路径长度WPL最小的二叉树 称为 哈夫曼树(最优二叉树)。

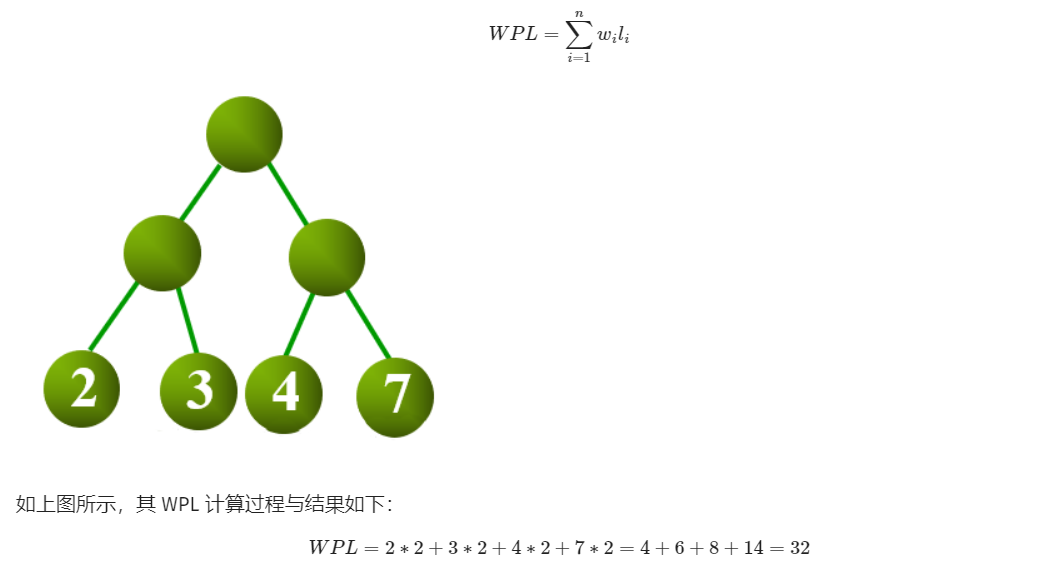
构造哈夫曼树的哈夫曼算法描述：

1. 初始化：根据给定的n个权值 {w₁ , w₂ , … , w_n }构成n棵二叉树集合 F = {T₁, T₂, … , T_n }， 其中每棵二叉树T_j 中只有一个带权的w_j 的根结点，其左右子树均为空
2. 选取与合并：在F中 选取两棵根结点的权值最小的树 作为左右子树(注意：相对较小的是左孩子，相对较大的是右孩子)构造一棵新的二叉树，且置新的二叉树的根结点的权值为其 左右子树上根结点的权值之和
3. 删除与加入：在F中删除 这两棵子树，同时将新得到的二叉树加入F中
4. 重复2和3步骤，直到F只含一棵树为止。这棵树就是 哈夫曼树

Huffman树特点：

• 权值最大的结点 离根最近，权值最小的结点 离根最远
• 树中没有度为1的结点
• 如果叶子结点的个数为n，那么树中共有 2n-1 个结点

赫夫曼编码

为了解决 远距离通信(主要是电报)的数据传输的最优化问题，提出了哈夫曼编码。

引例

对于一段报文，使用二进制编码进行网络传输

使用正常的01字符串进行等长编码，如下：

使用 赫夫曼编码(不等长编码)，如下：

定义

赫夫曼编码(Huffman Code)，其构造步骤如下：

1. 设需要编码的字符集为 {d₁ , d₂ , … , d_n }，各个字符在电文中出现的次数或者频率集合为 {W₁ , W₂ , … , W_n }
2. 以d₁ , d₂ , … , d_n 作为叶子结点，以W₁ , W₂ , … , W_n 作为相应叶子结点的权值来构造一棵哈夫曼树。
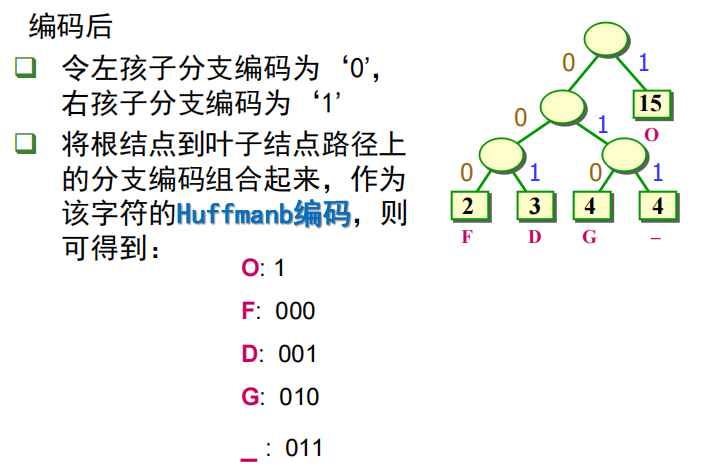
3. 规定哈夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为 该结点对应字符的编码

前缀编码：任何一个字符都不是另一个字符的编码的前缀。

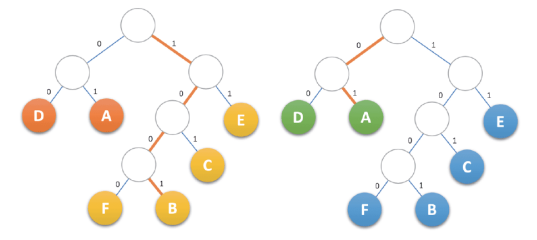
观察上图中的 “1001”(B)、“1000”(F)编码，可以发现从根结点到叶子结点的路径上，没有其他字符编码结点，也就是不存在 前缀为 “10"和 “100"的其他字符编码，故：Huffman是一种前缀编码，解码时不会混淆。

赫夫曼树实现

使用静态链表实现，结构如下：

1
2
3
4
5
6
7
8

typedef struct {
	ElemType data;
	unsigned int weight;
	unsigned int parent, lchild, rchild;
}HTNode, *HuffmanTree;  // 三叉链表结构体，三个指针分别指向赫夫曼树的左右孩子、双亲

typedef char** HuffmanCode;  // 这里HuffmanCode用二级指针，存储一个指针数组
// 数组的每个元素分别是一个指向 字符串首地址的指针，用于单独存储 字符的赫夫曼编码序列

设静态链表为 HT(含有2n个结点，其中n 为叶子结点数，0号单元未使用，构造n-1个parent结点)，过程如下：

1. 初始化：令所有单元的parent、lchild、rchild指针均指向0，设置 1~n 个结点的 data、weight(也就是最初的带有权值的叶子结点)
2. 从 i = n+1 开始，每次在 1~i-1(i-1是构造完parent新生成的树也放到集合中) 单元中选取 parent=0(代表一棵树的根结点)、且权值最小的两个结点，设为s₁、s₂，令 i 为此两结点的父结点，修改如下：

1
2
3
4

HT[s1].parent = i, HT[s2].parent = i;
HT[i].lchild = s1, HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
i++;

3. 重复步骤2，直到i = 2* n(最后一个结点的parent=0，代表构造生成的赫夫曼树根结点)

注：n个叶子结点的Huffman树共2n-1个结点。两两合并，直至一棵树，共生成n-1个结点。

赫夫曼树编码实现

对于每个带权值的待编码结点，从叶子结点开始出发，从叶子结点走到根结点的路径，记录其编码序列。

用字符数组 char code[n]存放单结点编码，由于n个初始待编码结点共生成n-1个parent结点，故从 叶子结点到根结点的路径长度 len<= n-1，字符数组code最后一个字符存放 ‘\0’，作为字符串结束标志，剩余 n-1个空间足够存放一个 待编码结点的编码序列。

从叶子结点出发走到根结点，倒序记录编码序列，使用指针start = n-1;初始化指向结尾空字符，每次存放字符时：code[--start] = '0'; 进行存储，最后每个字符的编码值为 code[start, ..., n-2]

代码框架：外层循环对 从1~n的叶子结点分别求其编码序列，存入字符数组code[n]中，每次求完一个完整的编码序列，将其拷贝到HuffmanCode二级指针数组中。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

// HuffmanTree 静态链表，存放待构建的赫夫曼树
// HuffmanCode 二级指针，存放n个字符最后的编码结果
// w 整型数组，存放n个字符的权值
// n 代表n个字符数量
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n) {
	if (n <= 1) return;
	int m = 2*n -1;
	HT = (HuffmanTree)malloc((m+1) * sizeof(HTNode));  // 0号下标 未使用
	
	// 先初始化赫夫曼树  静态链表
	for (int i = 1; i <= n; i++) {
		HT[i].weight = w[i-1];
		HT[i].parent = 0, HT[i].lchild = 0, HT[i].rchild = 0;
	}
	for (int i = n+1; i <= m; i++) {
		HT[i].weight = 0;
		HT[i].parent = 0, HT[i].lchild = 0, HT[i].rchild = 0;
	}
	
	// 构建赫夫曼树
	for (int i = n+1; i <= m; i++) {
		// 在HT[1, ..., i-1]中选择 parent=0，且weight最小的两个结点
		// 用序号s1, s2来记录其数组下标
		int s1, s2;
		Select(HT, i-1, s1, s2);  // 默认HT[s1].weight <= HT[S2].weight
		// 也就是s1作为新生成树的左子树根结点，s2作为新生成树的右子树根结点
		HT[s1].parent = i, HT[s2].parent = i;
		HT[i].lchild = s1, HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}
	
	// 从叶子结点 到根结点，逆向求 每个字符 单独的哈夫曼编码序列
	char *code = (char*)malloc(n*sizeof(char)); // 分配求编码的工作空间
	code[n-1] = '\0';
	// 逐个字符求哈夫曼编码
	for (int i = 1; i <= n; i++) {
		int start = n-1;
		for (int c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {
			// 从叶子 到根逆向 求编码
			if (HT[f].lchild == c) code[--start] = '0';
			else  code[--start] = '1';
		}
		HC[i] = (char*)malloc((n - start) * sizeof(char));
		// 为 第i个字符编码分配空间
		strcpy(HC[i], &code[start]);   // 将code字符数组中的 编码序列 拷贝到 HuffmanCode指针数组中
	}
	free(code);
	
}

赫夫曼解码

算法流程：

• 定义指针p指向 赫夫曼树结点，实际时记录结点数组的下标
• 定义指针i指向编码串，定义 ch 逐个去编码串的字符
• 初始化：读入编码串，设置p指向根结点，i=0
• 执行以下循环：
  1. 去编码串的第i个字符放入ch
  2. 如果 ch == '\0';，表示往左孩子移动，则p跳转到左孩子；如果ch == '\1'，表示往右孩子移动，则p跳转到右孩子
  3. 如果 ch非0非1，表示编码串有误，输入error表示编码失败，并且返回
  4. 检查p指向的结点是否为 叶子：
     • 如果是叶子，输出编码，p跳回根结点
     • 如果不是叶子，设置ch为3
  5. 继续循环，直到编码串 末尾
• 循环执行完毕，如果 ch==3;，输出解码失败，否则成功返回

小结

哈夫曼树和哈夫曼编码是 二叉树的一个应用。对带权路径的二叉树的学习，可以初步理解 数据压缩的原理，并且明白其是如何做到无损编码和无错编码的。

字典树(Trie树)

Trie 这个术语来自于 retrieval(检索)。根据词源学，trie 的发明者 Edward Fredkin 把它读作/ˈtriː/ “tree”。但是，其他作者把它读作/ˈtraɪ/ “try”。trie 中的键通常是字符串，但也可以是其它的结构。trie 的算法可以很容易地修改为处理其它结构的有序序列，比如一串数字或者形状的排列。比如，bitwise trie 中的键是一串位元，可以用于表示整数或者内存地址。trie 树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

附录

参考文献

• 《大话数据结构》
• 《算法笔记》
• MOOC 数据结构-浙江大学
• 霍夫曼树
• 树-前缀树(Trie)

版权信息

本文原载于kitebin.top，遵循CC BY-NC-SA 4.0协议，复制请保留原文出处。