基础算法精讲专题
01 相向双指针
167. 两数之和 II - 输入有序数组
双指针思路:
对于一个递增有序的数组来说,查找数组中两数之和=给定target的值,且整个数组只有唯一答案。
初始化双指针 i指向数组第一个元素,j指向数组最后一个元素,分类讨论如下:
- 当
numbers[i] + numbers[j] > target,说明 区间[i, j-1]中任何数和numbers[j]相加都大于target ,说明numbers[j]不是最终匹配的数,不考虑numbers[j],j--向前挪动指针,
- 当
numbers[i] + numbsers[j] < target,说明 区间[i+1, j]中任何数和numbers[i]相加都小于target,说明numbsers[i]不是最终匹配的数,不考虑numbers[i],i++向后挪动指针
- 当
numbers[i] + numbers[j] == target,匹配成功,退出循环
上述,双指针搜索过程中,利用了数组已按 非递减顺序排列这个性质,通过巧妙初始化两个前后指针,每次比较利用O(1)时间复杂度来==排除一个不符合条件的数字==(利用O(1)时间知道了数组中O(n)复杂度的信息,从而能够优化暴力解法),最终的时间复杂度优化为 O(n)
代码小细节:
-
循环退出条件:
-
返回值:
- 题目明确说明:这是 从下标1 开始的整数数组,例如: [2, 7, 11, 15] target=9,这里返回元素 2 7下标,从1开始就是返回 [1, 2],而数组下标默认从 0开始,故后面的返回值都要+1
完整代码如下:
C++代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
// 法一:暴力做法 时间复杂度 O(n^2)
// int i, j;
// for (i = 0; i < numbers.size(); ++i)
// for (j = 0; j < numbers.size(); ++j) {
// if ((numbers[i]+numbers[j]) == target)
// break;
// }
// return {i, j};
// 法二:双指针 时间复杂度 O(n)
// 注意:这是 从下标1 开始的整数数组
// [2, 7, 11, 15] target=9
// 这里返回 2 7下标,从1开始就是返回 [1, 2]
// 而数组下标默认从 0开始,故后面的返回值都要+1
int i = 0, j = numbers.size()-1;
// 由于题目给出了这个index范围1 <= index1 < index2 <= numbers.length,所以while循环可以退出条件可以写为如下:
// 当然 由于题目保证:每个输入都有唯一答案,所以也可以写:while(true)
while (i < j) {
if (numbers[i] + numbers[j] > target) j--;
else if (numbers[i] + numbers[j] < target) i++;
else break;
}
return {i+1, j+1};
}
};
|
15. 三数之和
双指针思路:
从上一题解法,可以知道,只要数组是有序的,就可以使用相向双指针来解
- 首先,先对
nums数组排序,调用:sort(nums.begin(), nums.end());
- 从后往前枚举:
nums[k],要使得:nums[i] + nums[j] + nums[k] = 0,等价于:nums[i] + nums[j] = -nums[k],那么问题就是在for循环中枚举nums[k]同时,进行两数求和
时间复杂度:外层for循环,套上里边双向指针每次O(n)时间复杂度,总的时间复杂度为O($n^2$)
代码小细节:
-
for循环这个k退出条件,一开始写k > 2,想着在数组中第0~2为的元素就是最后可能符合解了,但是有一个样例:nums = [0,0,0], 由于我这个判断不通过,不会进入循环,也就没有找出唯一解,为了解决这个问题,把k > 2改为 k>=2,把 控制三个数不相等放在后面while(i < j)中,由于 j初始化本来就比k 小1。所以 只要限制if(i < j),即可达到:i < j < k 的效果
-
注意到题目要求有答案中不可以包含重复的三元组,一开始没考虑导致样例不过:
1
2
3
4
|
nums = [0,0,0,0]
// 输出:[[0,0,0],[0,0,0]]
// 预期结果:[[0,0,0]]
// 解决:需要去重
|
后面发现这个要求后,先对数组进行了排序,故每次枚举i检查当前数 是否和前一个数相同,相同跳过; 每次枚举 j 检查当前数是否 和后一个数相同,相同跳过即可; 还有一个 枚举k也需要相同的检查,添加判断语句如下:
1
2
3
4
5
6
7
8
9
10
|
if (k < nums.size()-1 && nums[k] == nums[k+1]){
// 由于每次在 for循环中都会改变 k值,所以这里直接continue,不用改变k值
continue;
}
if (i > 0 && nums[i] == nums[i-1]) {
i++; continue;
}
if (j < k-1 && nums[j] == nums[j+1]) {
j--; continue;
}
|
由于这个三数之和可以有多个解,不像上述两数之和只有一个解,一开始只考虑一个解,while循环逻辑写成:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
while (i < j) {
if (i > 0 && nums[i] == nums[i-1]) {
i++; continue;
}
if (j < k-1 && nums[j] == nums[j+1]) {
j--; continue;
}
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
else break;
}
if (i < j)
vi.push_back({nums[i], nums[j], nums[k]});
|
即找到一个符合要求的两数之和等于-nums[k]我就break跳出循环了,实际上是需要继续枚举的,一开始没有考虑导致卡在这个样例[-1,0,1,2,-1,-4,-2,-3,3,0,4],这个样例比如nums[k]=-3,而nums[i], nums[j]可以有多种组合,修改上述代码while循环如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
while (i < j) {
if (i > 0 && nums[i] == nums[i-1]) {
i++; continue;
}
if (j < k-1 && nums[j] == nums[j+1]) {
j--; continue;
}
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
else {
vi.push_back({nums[i], nums[j], nums[k]});
i++, j--;
}
}
|
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
int i, j, k;
vector<vector<int>> vi;
// 枚举 nums[k]
// 要使得:nums[i] + nums[j] + nums[k] = 0
// 相当于:nums[i] + nums[j] = -nums[k]
// 转换成两数之和,使用双向指针求解
// 时间复杂度:O(n^2)
// 这里有个边界情况:k > 2时,样例:nums = [0,0,0]
// 由于判断不通过,不会进入循环,也就没有找出唯一解,为了解决这个问题,把k > 2改为 k>=2
// 把 控制三个数不相等放在后面 if (i < j)中,由于 j初始化本来就比k 小1
// 所以 只要限制if(i < j)即可达到:i < j < k 的效果
for (k = nums.size()-1; k >= 2; k--) {
i = 0, j = k-1;
if (k < nums.size()-1 && nums[k] == nums[k+1]){
// 由于每次在 for循环中都会改变 k值,所以这里直接continue,不用改变k值
continue;
}
while (i < j) {
if (i > 0 && nums[i] == nums[i-1]) {
i++; continue;
}
if (j < k-1 && nums[j] == nums[j+1]) {
j--; continue;
}
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
// 注意这里由于不是限制说只有一个解,所以需要一直循环,把所有满足条件解都找到
else {
// continue;
vi.push_back({nums[i], nums[j], nums[k]});
// 注意要改变一下 i, j的值,不然会死循环
i++; j--;
}
}
// if (i < j)
// vi.push_back({nums[i], nums[j], nums[k]});
}
return vi;
}
};
|
改进代码:
看了灵神讲解,发现只有在nums[i] + nums[j] + nums[k] = 0,就是找到一个解情况下,才需要考虑去重问题,所以在while(i < j)循环中,把去重的部分写到条件匹配语句中,可以避免很多不必要的判断
-
原来代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
while (i < j) {
if (i > 0 && nums[i] == nums[i-1]) {
i++; continue;
}
if (j < k-1 && nums[j] == nums[j+1]) {
j--; continue;
}
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
// 注意这里由于不是限制说只有一个解,所以需要一直循环,把所有满足条件解都找到
else {
// continue;
vi.push_back({nums[i], nums[j], nums[k]});
// 注意要改变一下 i, j的值,不然会死循环
i++; j--;
}
}
|
-
改进代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
while (i < j) {
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
// 注意这里由于不是限制说只有一个解,所以需要一直循环,把所有满足条件解都找到
else {
// continue;
vi.push_back({nums[i], nums[j], nums[k]});
// 注意要改变一下 i, j的值,不然会死循环
i++;
while(i < j && nums[i] == nums[i-1]) {
i++; // 这里找到一个符合的nums[i]了,执行过i++, i > 0一定成立
}
j--;
while(j > i && nums[j] == nums[j+1]) {
j--; // 这里找到一个符合的nums[j]了,执行过j--,j < k-1一定成立
}
}
}
|
另外有两个小优化:
-
如果 nums[k] 和离他最近的两个最大的数相加小于0,即:nums[k]+nums[k-1]+nums[k-2] < 0,可以直接break中止掉了,后面的枚举都不会有解了
-
如果nums[k]和剩余数字中最小的两个数相加大于0,即:nums[k]+nums[i]+nums[i+1] > 0,那么可以枚举下一个nums[k]了,在[i, j]中找"两数之和"了
-
添加代码如下:
1
2
3
4
|
if (k >= 2 && nums[k]+nums[k-1]+nums[k-2]<0)
break;
if (k >= 2 && nums[i]+nums[i+1]+nums[k]>0)
continue;
|
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
int i, j, k;
vector<vector<int>> vi;
for (k = nums.size()-1; k >= 2; k--) {
i = 0, j = k-1;
if (k < nums.size()-1 && nums[k] == nums[k+1]){
// 由于每次在 for循环中都会改变 k值,所以这里直接continue,不用改变k值
continue;
}
if (k >= 2 && nums[k]+nums[k-1]+nums[k-2]<0)
break;
if (k >= 2 && nums[i]+nums[i+1]+nums[k]>0)
continue;
while (i < j) {
if(nums[i] + nums[j] < -nums[k]) i++;
else if(nums[i] + nums[j] > -nums[k]) j--;
// 注意这里由于不是限制说只有一个解,所以需要一直循环,把所有满足条件解都找到
else {
// continue;
vi.push_back({nums[i], nums[j], nums[k]});
// 注意要改变一下 i, j的值,不然会死循环
i++;
while(i < j && nums[i] == nums[i-1]) {
i++; // 这里找到一个符合的nums[i]了,执行过i++, i > 0一定成立
}
j--;
while(j > i && nums[j] == nums[j+1]) {
j--; // 这里找到一个符合的nums[j]了,执行过j--,j < k-1一定成立
}
}
}
}
return vi;
}
};
|
课后作业
16.最接近的三数之和
18.四数之和
2824.统计和小于目标的下标对数目
611.有效三角形的个数
02相向双指针
11. 盛最多水的容器
双指针思路:
面积公式:S(i,j)=min(h[i],h[j])×(j−i)
-
一开始初始化两个指针指向 数组两端left right,盛水容量取决于 高度较低的那一端
-
在数组中间[left, right] 范围内随便挑选一个下标为 k 的高度和较短的 一端构成容器
height[k] < min(height[left], height[right]):由于底边长 < 原变长 ,故容量小于原来的体积height[k] > min(height[left], height[right]):由于底边长 < 原变长,高度取决于短的一段,故容量小于原来的体积
-
通过上面的分析,可以发现:height[left]和height[right]中短的一段保留移动 另一端已经无法获得比当前更大容量,移动指向高度较短的一端的指针,放弃较小边,以获得较高边-较大容量的机会
时间复杂度分析:O(n);空间复杂度分析:O(1)
对比暴力枚举:水槽两板围成面积 S(i,j) 的状态总数为C(n,2)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size()-1;
int maxVal = 0;
while (left < right) {
maxVal = max(maxVal, min(height[left], height[right]) * (right - left));
if (height[left] > height[right]) right--;
else left++;
}
return maxVal;
}
// 更加优雅写法
int maxArea1(vector<int>& height) {
int i = 0, j = height.size() - 1, res = 0;
while(i < j) {
res = height[i] < height[j] ?
max(res, (j - i) * height[i++]):
max(res, (j - i) * height[j--]);
}
return res;
}
};
|
42. 接雨水
算法思路:
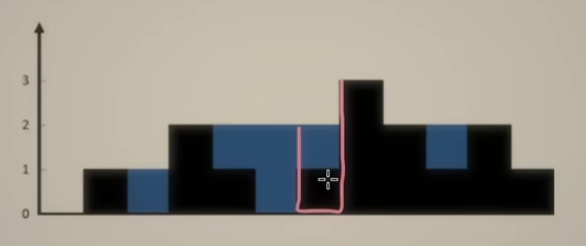
如上图,要求每个柱子所能接多少雨水,取决于当前柱子左边隔板最大高度 与 右边隔板最大高度,两个最大高度中取最小值,乘上柱子边长减去柱子本身高度,即为:柱子所能接收雨水的量。
按照上述的思路,这道题可以使用前后缀最大值的思路来求解,下面两种方法:
- 方法一是使用两个数组来存储前后缀最大值,然后通过再遍历一遍数组,获取所有柱子所能接收雨水的量;
- 方法二则是使用双指针,本质上是用两个常量保存当前指针 所指柱子前后缀最大值,节省了数组空间。
前后缀分解预处理代码:
1
2
3
4
5
6
7
8
9
|
vector<int> pre_max; // 创建两个数组,用于存储前缀最大值 和 后缀最大值
pre_max.push_back(height[0]);
int size = height.size();
for (int i = 1; i < size; ++i)
pre_max.push_back(max(pre_max[i-1], height[i]));
vector<int> suf_max(size, 0);
suf_max[size-1] = height[size-1];
for (int i = size-2; i >= 0; --i)
suf_max[i] = max(suf_max[i+1], height[i]);
|
时间复杂度:O(n);空间复杂度:O(n)
双指针思路:
不同于上述前后缀数组的预处理,这里需要思考一下如何移动两个指针的问题?
假设左边指针 指向的柱子的左边的部分前缀最大和已知,右边指针指向的柱子的右边的部分后缀最大和已知,如下图:
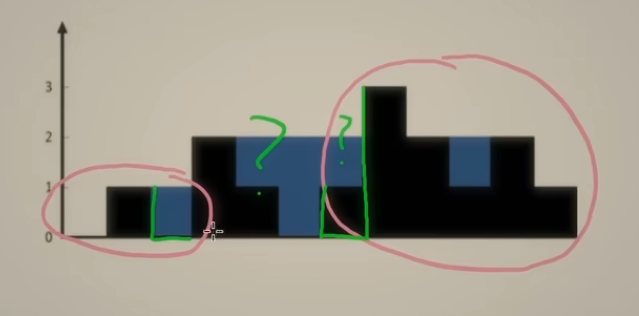
- 对于==右边绿线描绘的柱子==,右边后缀最大和已知,左边部分后缀最大和也已知,由于柱子的容量总是有 最短木板效应,若是 右边后缀最大和 < 左边部分后缀最大和,而左边部分后缀最大和总是非递减的,此时可以直接计算==右边绿线柱子==所能接水容量,然后 右指针向左移动
- 对于==左边绿线描绘的柱子==,左边后缀最大和已知,右边部分后缀最大和已知,由于柱子的容量总有 最短木板效用,若是 左边后缀最大和 < 右边部分后缀最大和,而右边部分后缀最大和也是非递减的,此时可以直接计算==左边绿线柱子==所能接水容量,然后 左指针 向右移动
时间复杂度:O(n);空间复杂度:O(1)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
int trap(vector<int>& height) {
int preMax = 0, sufMax = 0;
int left = 0, right = height.size()-1;
int ans = 0;
// 双指针这里不需要等号吧,如果等于的时候还有容量,
// 说明这个位置两边必定有大于该位置的数,那么在循环过程中就会先计算这个位置了
// 不加等号也是可以的,最后必定会停在一个无法接水的位置。
while (left <= right) {
preMax = max(preMax, height[left]);
sufMax = max(sufMax, height[right]);
if (preMax < sufMax) {
ans += preMax-height[left++];
} else {
ans += sufMax-height[right--];
}
}
return ans;
}
int trap1(vector<int>& height) {
vector<int> pre_max; // 创建两个数组,用于存储前缀最大值 和 后缀最大值
pre_max.push_back(height[0]);
int size = height.size();
for (int i = 1; i < size; ++i)
pre_max.push_back(max(pre_max[i-1], height[i]));
vector<int> suf_max(size, 0);
suf_max[size-1] = height[size-1];
for (int i = size-2; i >= 0; --i)
suf_max[i] = max(suf_max[i+1], height[i]);
int ans = 0;
for (int i = 0; i < size-1; ++i)
ans += (min(pre_max[i], suf_max[i]) - height[i]);
return ans;
}
};
|
注:一般把窗口大小不固定的技巧称为 双指针,大小固定的技巧称为 滑动窗口。
03 同向双指针 滑动窗口
209. 长度最小的子数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
// 时间复杂度:O(n)
// 空间复杂度:O(1)
int minSubArrayLen(int target, vector<int>& nums) {
int size = nums.size();
int ans = size+1, left = 0;
int sum = 0;
for (int i = 0; i < size; ++i) {
sum += nums[i];
// 单调性:
// 对于本题而言,left移动时,子数组的和是在不断变小的
// while循环里边的条件不断变化,从满足要求——> 不满足要求
// 只有满足了 单调性,才可以使用双指针
while(sum >= target) {
ans = min(ans, i - left + 1);
sum -= nums[left];
left += 1;
}
}
return ans <= size ? ans : 0;
// if (ans == size+1)
// return 0;
// else
// return ans;
}
};
|
713. 乘积小于 K 的子数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Solution {
public:
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
// 暴力解法:由于每次 right = left 指针回溯
// 故时间复杂度为:O(n^2)
int len = nums.size();
int ans = 0;
int product = 1;
int left = 0, right = left;
while (left < len) {
while (right < len && product * nums[right] < k) {
ans += 1;
product *= nums[right];
right++;
}
left++; right = left;
product = 1;
}
return ans;
}
int numSubarrayProductLessThanK1(vector<int>& nums, int k) {
// 固定右端点,从 0 开始拓展,用下标 right 表示,表示 以right 为结尾的子数组
// 左端点默认从 0 开始
// 这里需要使用前缀 成绩数组预处理一下 这样就需要开一个 n大小数组,空间复杂度过高
// 从上面 由左到右 遍历的话,前缀乘积数组可以暂时 用一个sumProduct 暂存,这样就可以达到O(1)时间复杂度
// 加速代码如下
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
if (k <= 1) return 0; // 特判,防止 后面循环出错
int len = nums.size();
int ans = 0;
int product = 1;
int right = 0, left = 0;
while (right < len) {
product *= nums[right];
// 这里循环 product >= k要保证 left <= right,前提是:k <= 1
while (product >= k) {
product /= nums[left++];
}
ans += (right - left + 1);
right++;
}
return ans;
}
};
|
3. 无重复字符的最长子串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
int lengthOfLongestSubstring(string s) {
map<char, int> mp;
int ans = 0;
int r = 0, l = 0;
while (r < s.length()) {
if (mp.count(s[r]) > 0)
mp[s[r]] += 1;
else mp[s[r]] = 1;
while (mp[s[r]] > 1) {
mp[s[l++]] -= 1;
}
ans = max(ans, r-l+1);
// 注意 r++,否则会出现 死循环问题
r++;
}
return ans;
}
};
|
课后作业
1004.最大连续 1 的个数 III
1234.替换子串得到平衡字符串
1658.将 x 减到 0 的最小操作数
2962.统计最大元素出现至少 K 次的子数组
04 二分查找 红蓝染色法
二分查找讲解
二分查找在 闭区间上的写法,对比开区间 和 半闭半开区间 三种写法的区别
问题: 返回 有序数组中第一个 $\geq$ 8的数的位置,如果所有数都 < 8,返回数组长度

暴力做法: 遍历每个数,询问它是否 $\geq$ 8 ?
高效做法:
解法一(左闭右闭)
上述暴力做法没有利用到 数组是有序这个性质,在解题时考虑数组有序性质。初始化两个指针,L和R分别指向询问的左右边界,即:闭区间[L, R], M指向当前正在询问的数
- 红色背景:表示false,即:< 8
- 蓝色背景:表示true,即:$\geq$ 8
- 白色背景:表示不确定
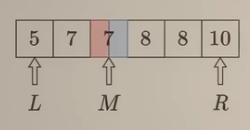
-
M是==红色== => [L, M]都是==红色==,剩余不确定的区间为 [M+1, R]。因此下一步 $L \space \longleftarrow \space M+1$,这同时也说明: L-1 指向的一定是==红色==。 (注:如果改成 L = M,就变成 左开右闭 区间进行处理,这种做法会导致死循环)

-
继续询问
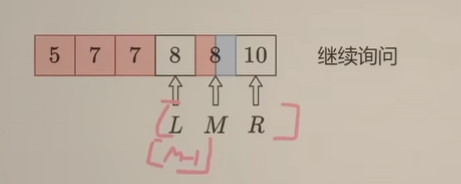
-
M是 ==蓝色== => [M, R]都是 ==蓝色==,剩余不确定的区间为 [L, M-1 ]。因此下一步 $R \space \longleftarrow \space M-1$ ,这同时也说明:R+1 指向一定是==蓝色==,更新如下:
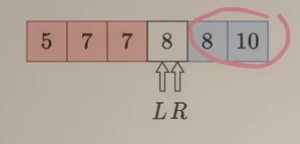
-
继续询问
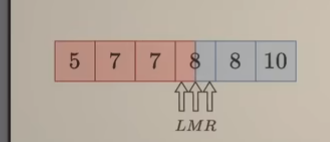
-
继续更新R,此时:R < L,循环结束。此时要查找的数是哪个指针指向的下标呢? 注意循环不变量
- L - 1 始终是 ==红色==
- R + 1始终是 ==蓝色==
根据循环不变量,可以知道R + 1就是我们要找的答案。由于循环结束后,R + 1 = L,所以答案也可以用L表示
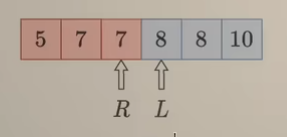
解法二(左闭右开区间)
把区间的左端点 或者 右端点,当成是开区间,例如:初始化R = length,指向数组最后一个元素的后一个位置,注意几个分支中 L、R指针的移动条件:
nums[mid] >= target:R = M; // 这里缩小区间为 [L, M),故可以把 R直接用M赋值nums[mid] < target:L = M+1; // 这里缩小区间为 [M+1, R),需要把左端点赋值给L- 当 L = R时,左闭右开区间 没有元素了,情况结束,所以while的循环条件为:
L < R,此时L 与R指针都是指向 所要找的区间端点答案,直接返回即可
解法三(左开右开区间)
思路类似解法二,只需要把条件分支修改L指针,改成L = M; 接着把while循环条件写成:while(L + 1 < R)即可。
小结
如何处理:$\geq \space > \space < \space \leq$ 这四种情况,最后解决题目
上述的解法针对的题目背景如下:
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
上述的思路都是在讲解:在数组nums中找到一个最左边的下标low,有:nums[low] >= target,解法一左闭右闭区间的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// 左闭右闭 区间写法
// while循环条件为:left <= right
std::function<int(vector<int>, int)> lower_bound = [&] (vector<int> nums, int target){
int left = 0, right = nums.size()-1; // 闭区间[left, right]
while (left <= right) { // 区间不为空
// left + (right - left) / 2 这种写法可以防止整数溢出问题
// 普通写法:mid = (left + right) / 2
int mid = (left + right) / 2;
if (nums[mid] < target) {
left = mid + 1; // [mid+1, right]
} else {
right = mid - 1; // [left, mid-1]
}
}
return left;
};
|
接口参数说明:lower_bound(vector<int> nums, int target);,这里返回值是找到数组中从左往右数 第一个nums[low] >= target的下标 low。
而其他三种情况:找到数组中从左往右数 第一个nums[low] > target下标、找到数组中从右往左数 第一个nums[low] <= target下标、找到数组中从左往右数 第一个nums[low] < target的下标,都可以由上述这种情况来转换:
- 情况一:
low1 = lower_bound(nums, target + 1);,low即为所求的下标
- 情况二:
low2 = lower_bound(nums, target + 1) - 1;, low即为所求的下标
- 情况三:
low3 = lower_bound(nums, target) - 1;, low即为所求的下标
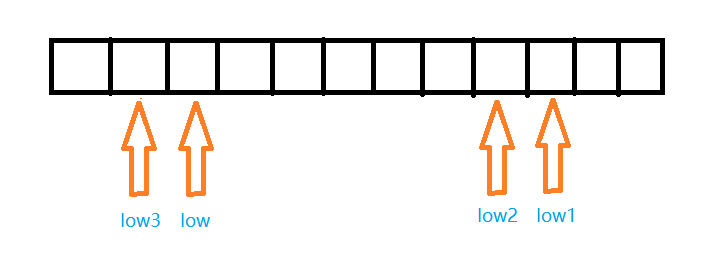
上面的情况就是如上的数组,闭区间 [low, low2]中的元素都等于target,nums[low3]是指向第一个小于target的数,nums[low1]是指向第一个大于target的数
34. 在排序数组中查找元素的第一个和最后一个位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
// 左闭右闭 区间写法
// while循环条件为:left <= right
std::function<int(vector<int>, int)> lower_bound = [&] (vector<int> nums, int target){
int left = 0, right = nums.size()-1; // 闭区间[left, right]
while (left <= right) { // 区间不为空
// left + (right - left) / 2 这种写法可以防止整数溢出问题
// 普通写法:mid = (left + right) / 2
int mid = (left + right) / 2;
if (nums[mid] < target) {
left = mid + 1; // [mid+1, right]
} else {
right = mid - 1; // [left, mid-1]
}
}
return left;
// No viable conversion from '(lambda at /mnt/g/CodeFile/CODE_CPP/Data-Structure/Basic/LC-BasicAlgorithm/34.在排序数组中查找元素的第一个和最后一个位置.cpp:13:60)' to 'std::function<int (vector<int>, int)>'
// 注意:一个函数没有 特定类型的返回值,lambda表达式会上面这个错误
// return 1;
};
// 左闭右开 区间写法
// while循环条件为:left < right
std::function<int(vector<int>, int)> lower_bound2 = [&] (vector<int> nums, int target) {
int left = 0, right = nums.size(); // 左闭右开 [left, right)
while (left < right) { // 区间不为空
// left + (right - left) / 2 这种写法可以防止整数溢出问题
// 普通写法:mid = (left + right) / 2
int mid = (left + right) / 2;
if (nums[mid] < target) {
left = mid + 1; // [mid+1, right)
} else {
right = mid; // [left, mid)
}
}
return left;
};
// 左开右开 区间写法
// while循环条件为:left+1 < right
std::function<int(vector<int>, int)> lower_bound3 = [&] (vector<int> nums, int target) {
int left = -1, right = nums.size(); // 左开右开 (left, right)
while (left+1 < right) { // 区间不为空
// left + (right - left) / 2 这种写法可以防止整数溢出问题
// 普通写法:mid = (left + right) / 2
int mid = (left + right) / 2;
if (nums[mid] < target) {
left = mid; // (mid, right)
} else {
right = mid; // (left, mid)
}
}
return left;
};
int start = lower_bound(nums, target);
// 表明数组中 没有目标的等于 target的元素
if(start == nums.size() || nums[start] != target)
return {-1, -1};
int end = lower_bound(nums, target + 1) - 1;
// 如果说 start存在,则end一定会有解,直接返回即可
return {start, end};
}
// 时间复杂度:取决于 lower_bound的复杂度,由于每次都是去掉数组的一半元素
// 所以这里 数组不断减半,时间复杂度为O(logn)
};
|
课后作业
搜索插入位置 https://leetcode.cn/problems/search-insert-position/
二分查找 https://leetcode.cn/problems/binary-search/
H 指数 II https://leetcode.cn/problems/h-index-ii/
05 二分查找 搜索旋转排序数组
对于红蓝染色法:
- right 左移使右侧变蓝 (判断条件为 true )
- left 右移使左侧变红 (判断条件为 false )
- 故确定二分处 ( mid ) 的染色条件是关键
注意:红蓝染色的交界处才是 二分查找 目标求解的分界点处。
162. 寻找峰值
下面采用二分查找—左开右开区间写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
// 疑问:右边界要初始成为n - 2(如果用闭区间的话),这个是怎么想到的呢?
// 答:因为 n-1 要么是答案,要么在答案右侧,所以 n-1 一定是蓝色,无需二分。
// 对于红蓝染色法 区间的说明:
// 区间表示【不知道要染成红色还是蓝色】的下标组成的范围。
// 如果区间内全为红色,那么答案自然就是 n-1。
// 按照定义,n-1 要么是峰顶,要么在峰顶右侧,所以一定染成蓝色,自然就不需要在初始的区间内了。
// 时间复杂度:O(logn)
// 空间复杂度:O(1)
int findPeakElement(vector<int>& nums) {
// 二分范围:[0, n-2]
// 开区间为:(-1, n-1)
int left = -1, right = nums.size()-1;
while (left + 1 < right) {
int mid = left + (right - left)/2;
if (nums[mid] > nums[mid+1]) // 蓝色
right = mid;
else
left = mid;
}
// 这里说明为何要 return right
// 看while循环中分支判断条件:
// 只有 nums[mid] > nums[mid+1]的时候,将right更新为mid
// 这里说明:right总是想着峰顶靠近,最后到达封顶的下标位置
return right;
}
};
|
153. 寻找旋转排序数组中的最小值
红蓝染色法:
- 红色: 表示 false,即 最小值左侧
- 蓝色:表示true,即最小值及其右侧
根据这一定义,n - 1必然是蓝色的
这样分析下来,这一题可以和上一题一样,在[0, n-2]中二分:
-
nums[mid] < last:那么有两种情况:
无论哪种情况,这个元素要么是最小值,要么在最小值右侧,这种情况下染成蓝色
-
nums[mid] > last:那么只有一种情况:
- 排除
nums[mid]在左边(只有 一段递增数组)
- 之呢个在 两段递增数组中的 前一段
说明,这个元素nums[mid]一定在最小值左侧,这种情况染成红色
那么二分范围 和 染色规则确定了,可以写代码了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int findMin(vector<int>& nums) {
// [0, n-2]
// (-1, n-1)
// 采用 左开右开 写法,注意初始化,刚刚初始化left = 0样例过不了了
int left = -1, right = nums.size()-1;
while (left+1 < right) {
// int mid = left + (right - left) / 2;
int mid = (left + right) / 2;
if (nums[mid] < nums[nums.size()-1])
right = mid;
else
left = mid;
}
// 返回 指针left 或者 right,得看情况
// right改变分支时,判断语句是:nums[mid] < nums[nums.size()-1]
// 这说明:mid 指向元素在 最小元素的右侧,或者就是最小元素
// 等到循环停止时,right恰好指向的是最小元素,直接返回nums[right]
return nums[right];
}
};
|
33. 搜索旋转排序数组
**法一:**两次二分
算法思路:
结合上一题,首先先 寻找旋转排序数组中的最小值,然后再一次二分在一段 升序的序列中寻找target目标值。
两次二分的时间复杂度都为O(log n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public:
// 法一:结合上一题:寻找旋转排序数组中的最小值,一次二分找到最小值分界点
// 然后接下来看 target在哪个升序区间范围内,再一次二分进行查找
int search(vector<int>& nums, int target) {
int left = -1, right = nums.size()-1;
while (left+1 < right) {
// int mid = left + (right - left) / 2;
int mid = (left + right) / 2;
if (nums[mid] < nums[nums.size()-1])
right = mid;
else
left = mid;
}
if(target < nums[right]) return -1;
int l, r;
// target <= last,表明:target在数组中 第二段递增区间
// target > last, 表明:target在数组中,第一段递增区间
if(target <= nums[nums.size()-1]) {
l = right, r = nums.size()-1;
} else {
// 这里的 l r初始化没有考虑到一下这种情况
// nums = [1] ; target = 1
// 考虑到的是 nums[right]左边还有 元素情况
// 万一 nums[right]就是最小值,左边已经没有元素,就会因为没进入循环,误判
// 添加特判样例
// 或者 像上面的if判断语句修正:target < nums[nums.size()-1] => target <= nums[nums.size()-1]
l = 0, r = right -1;
}
while(l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target)
return mid;
else if(nums[mid] < target) {
l = mid+1;
} else {
r = mid-1;
}
}
return -1;
}
};
|
法二: 一次二分
**算法思路:**分三种情况讨论,
【第一种情况】什么时候nums[mid]在 target及其右侧,这种情况染成蓝色;
- 如果
nums[mid]比最后一个元素大,说明nums[mid]在左边升序数组这一段,若此时target 也大于最后一个数,那么target与nums[mid]在同一段,并且此时nums[mid] >= target(说明nums[mid]在target及其右侧),那么 mid及其右侧都染成蓝色
【第二种情况】nums[mid]小于等于最后一个数,那么nums[mid]在右边升序数组这一段,此时 target 大于等于最后一个数,target在左边这一段,mid及其右侧也染成蓝色
【第三种情况】 (情况二不成立,target在第二段) nums[mid]大于等于 target,那么也是蓝色
其余情况,染成红色,为了方便:这里把判断蓝色的逻辑写成一个函数法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
int search(vector<int>& nums, int target) {
std::function<bool(int)> is_blue = [&] (int i) {
int end = nums[nums.size()-1];
if(nums[i] > end) {
return target > end && nums[i] >= target;
} else {
return target > end || nums[i] >= target;
}
};
int left = -1, right = nums.size();
while (left + 1 < right) {
int mid = (left + right) / 2;
if(is_blue(mid))
right = mid;
else
left = mid;
}
if(right == nums.size() || nums[right] != target)
return -1;
return right;
}
};
|
课后作业
154.寻找旋转排序数组中的最小值 II
06 反转链表 K个一组翻转
206. 反转链表
算法思路:
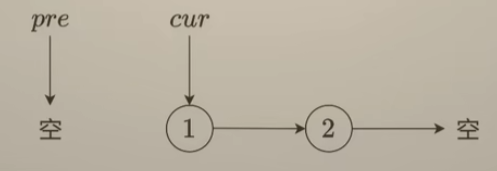
如上图所示,链表每个结点都包含:val(节点值)和指向下一个结点的next指针。
想要反转链表,常见思路是使用两个指针:
- pre指向当前结点的前一个结点
- cur指向 当前结点
修改当前cur的next指针指向pre指针指向的前向结点cur->next = pre;,这样就达到了将当前cur指针指向结点next值 “反转"的目的,不过由于直接将cur->next = pre;,若是没有记录指向后续指针结点,那就找不到下一个要"反转"的结点,故需要添加多一个指针nxt,指向当前指针的下一个结点,如下:
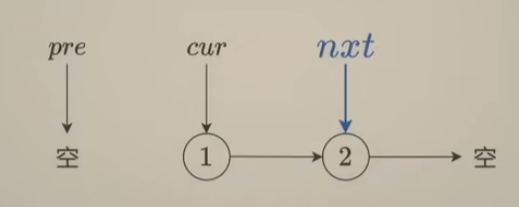
修改当前结点的next指针,指向前向结点,如下:
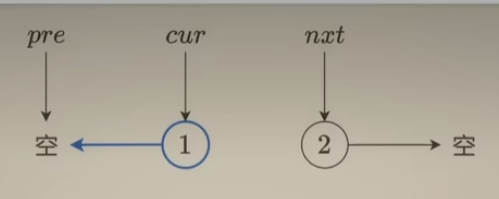
接着,更新cur值和pre值,准备对下一个结点进行"反转”,如下:
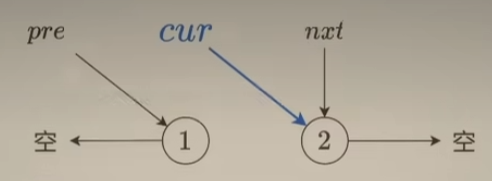
如此循环直到把所有结点都修改完,如下:
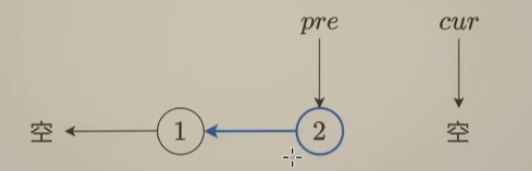
反转结束后,从原来链表上看:
- pre:指向反转这一段的末尾
- cur:指向反转链表末尾的下一个节点
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
// 自己的写法
ListNode* reverseList(ListNode* head) {
// head = [1,2,3,4,5]
// cout << head->val << endl;s
// 输出:1
if(head == nullptr)
return head;
ListNode *p = head->next, *q = nullptr;
while(p) {
head->next = q;
q = head, head = p;
p = p->next;
}
if(head) head->next = q;
return head;
}
// 博主的思路
// 执行用时:击败100% 用户
ListNode* reverseList1(ListNode* head) {
ListNode *pre = nullptr;
ListNode *cur = head, *nxt = nullptr;
while(cur) {
nxt = cur->next;
cur->next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
};
|
92. 反转链表 II
算法思路:
想要反转 链表中部分结点,应该如何做?
==记住重要性质==:
- pre:指向反转这一段的末尾
- cur:指向反转链表末尾的下一个节点
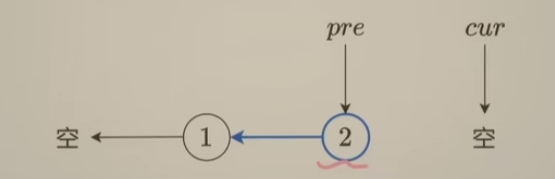
具体来看下面这个示例:
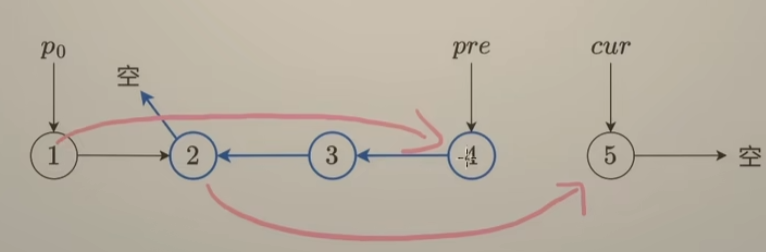
按照第一题的性质,中间一段反转之后,结点2的next值指向nullptr,此时pre指针指向结点4、cur指针指向结点5,增加的操作:
- 将结点2的next值指向cur指针指向的结点
- 将结点1的next值指向pre指针指向的结点
==特殊情况==:当left=1,即要反转的一段链表的第一个结点就是头结点时,没有上面的$p_0$所指向的结点,此时可以在原链表 head头结点前面加上一个哨兵结点,如下:

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
// 初始化哨兵结点,next值指向 head
ListNode *dummy = new ListNode(-1, head);
ListNode *p0 = dummy;
// p0指向要反转链表部分 第一个结点的上一个结点
for(int i = 0; i < left-1; ++i)
p0 = p0->next;
ListNode *pre = nullptr;
ListNode *cur = p0->next, *nxt = nullptr;
int len = right - left + 1;
for(int i = 0; i < len; ++i){
nxt = cur->next;
cur->next = pre; // 核心,每次反转修改的 指针指向
pre = cur;
cur = nxt;
}
p0->next->next = cur;
p0->next = pre;
// 若是返回head,当left=1,会被一下案例卡住测试
// [3,5]
// left=1, right=2
// [5,3]
// 故需要返回 dummy哨兵结点指向的下一个结点 (保证为链表的头结点)
return dummy->next;
}
|
25. K 个一组翻转链表
思路和上一题92一致,补充的操作:把p0更新成下一段要翻转的链表的前一个节点
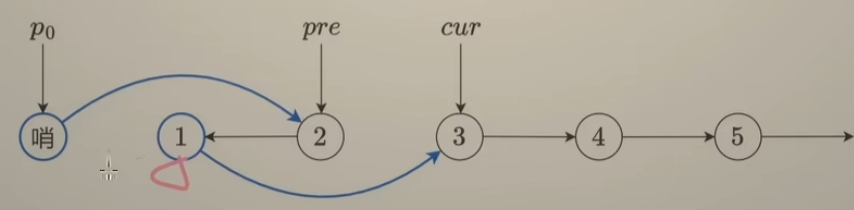
如上图:由于翻转K个结点之后,结点1变成了 要翻转的链表的前一个结点,即是p0->next原来的值,由于翻转过程中会修改p0->next,故:
提前创建一个临时变量 nxt = p0->next;,最后更新p0 = nxt;,开启下一轮循环。
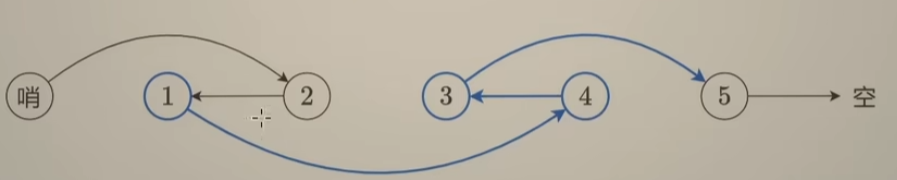
如上图,最后修改整个链表之后,发现哨兵结点的next值,即是链表的头结点!!!
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
int num = 0;
ListNode *p = head;
// 首先获取链表结点数 num
while(p) {
num++;
p = p->next;
}
// 初始化哨兵结点,next值指向 head
ListNode *dummy = new ListNode(-1, head);
ListNode *p0 = dummy;
// 这里 pre, cur, nxt指针初始化可以放在循环外部
// 从内层循环分析,每次翻转K个结点之后,cur恰好指向下一组K个结点中第一个结点位置
// nxt 在进入循环就 赋值给下一组K个结点的 下一个结点
// pre虽然没有能每次都在 cur指向结点前一个结点,但是其初始值并不会影响什么
// 一开始 将pre赋值给 第一个结点的next指针,后面翻转最后一步 第一个结点的Next指针也需要重新赋值
// 所以没有任何影响
ListNode *pre = nullptr;
ListNode *cur = p0->next, *nxt = nullptr;
while(num >= k) {
num -= k;
for(int i = 0; i < k; ++i){
nxt = cur->next;
cur->next = pre; // 核心,每次反转修改的 指针指向
pre = cur;
cur = nxt;
}
nxt = p0->next;
p0->next->next = cur;
p0->next = pre;
p0 = nxt;
}
// K个一组翻转链表之后, 哨兵结点dummy 的next还是指向头结点
// 上面p0 一开始赋值就是哨兵结点,也有参与指针运算
return dummy->next;
}
};
|
课后作业
24.两两交换链表中的节点
445. 两数相加 II
2816.翻倍以链表形式表示的数字
07 快慢指针 环形链表 重排链表
876. 链表的中间结点
简单思路:
遍历一遍链表求得 链表结点个数len,求中间结点编号 mid = len/2 + 1;,然后从head结点1开始遍历到mid结点即可返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* middleNode(ListNode* head) {
ListNode *p = head;
int len = 0; // 由于最后p = nullptr才退出,从p = head到p = nullptr,一共经过结点个数就是长度
while(p) {
p = p->next;
len++;
}
int mid = len / 2 + 1;
p = head;
for (int i = 2; i <= mid; ++i){
p = p->next;
}
return p;
}
};
|
快慢指针思想:
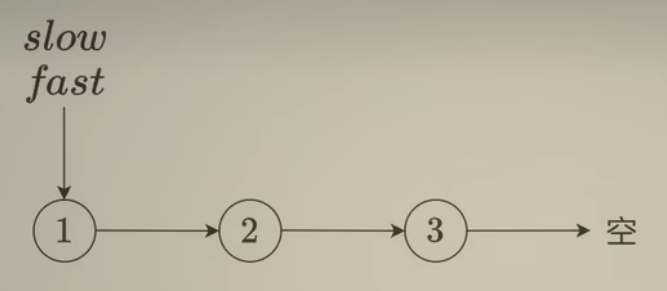
如上图,初始化两个指针slow和fast指针指向头结点,每次循环:快指针走两步,慢指针走一步。
比如长度为3的时候,循环一次后,慢指针指向中间结点,如下:
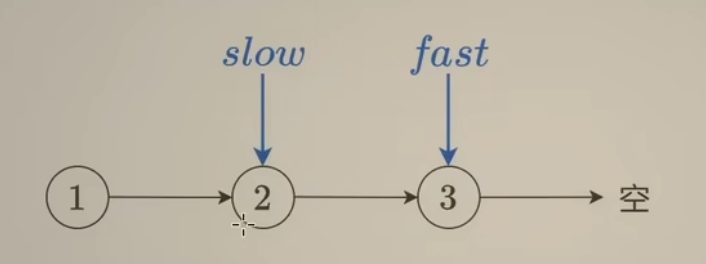
可以通过数学归纳法,证明:
- 奇数长度链表:快指针指向最后一个结点时,慢指针指向的恰好是中间结点
- 偶数长度链表:快指针指向空,慢指针一定在其规定的中间结点上

完整代码:
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public:
ListNode* middleNode(ListNode* head) {
ListNode *slow = head, *fast = head;
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
};
|
141. 环形链表
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
class Solution {
public:
// 思路一:暴力 数据范围 10^4,那么走 10^4 次还没走到头就是有环了
// 思路二:快慢指针
// fast 和 slow指针 同时开始
// 每次 fast指针移动两个结点,slow指针移动一个结点
// 当 fast 追上 slow 有环,反之如果 fast直接指向nullptr末尾,无环
// 进阶:你能用 O(1)(即,常量)内存解决此问题吗?
bool hasCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if(fast == slow)
return true;
}
return false;
}
};
|
上面说明:当fast追上slow指针时,说明该单链表中存在环。不过这暗示着,slow指针一定会走到环里边,这是两个指针相遇的充分必要条件。用相对速度思考,fast指针相对于slow指针每次循环都走一步,最后若是存在环,fast指针会循环回来 遇上 slow指针。
- 时间复杂度:由于slow指针 进入环后,循环次数 < 环的长度,故复杂度为O(n)
- 空间复杂度:O(1)
142. 环形链表 II
代码思路:
这题不仅需要判断是否有环,还需要找到 环的入口
设 头结点到入口距离为a,入口到相遇点 距离为b,相遇点到入口的距离为c
首先这里有个结论:当快慢指针相遇时,慢指针还没有走完一整圈
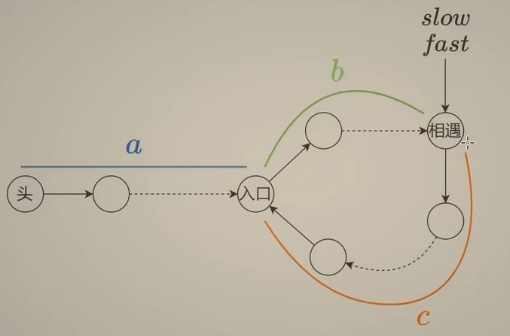

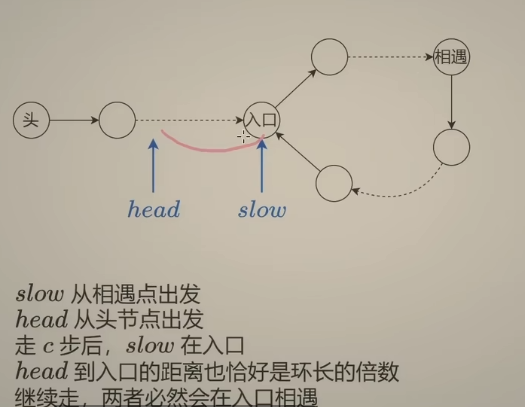
思考:快慢指针第一次相遇时,为什么慢指针 的移动距离小于环长?
- 最好情况:慢指针 入环就和快指针 相遇
- 最坏情况:慢指针第一次进入环时,快指针刚好在慢指针前面,用相对速度分析:快指针需要 走(环长 - 1)步 之后,才能与慢指针相遇。对于任何其他情况,快指针走的距离都不会超过(环长 - 1)步,可以推导出,慢指针移动的距离一定是小于环长的。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/**
* Definition for singly-linked list.
**/
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
class Solution {
public:
// 法一:哈希表+ 设定一个最多循环次数
// 法二:利用快慢指针相对的 速度,通过数学推导来找环 入口
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while(fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if(fast == slow) {
while(slow != head){
slow = slow->next;
head = head->next;
}
return slow;
}
}
return nullptr;
}
};
|
143. 重排链表
代码思路:
首先找到中间结点3,然后把中间结点后边这段 链表反转,得到如下的顺序:5->4->3,结合之前讲的链表的中间结点 以及 上面的 反转链表 来完成这两步,得到两段方向指向不同的链表,如图1:
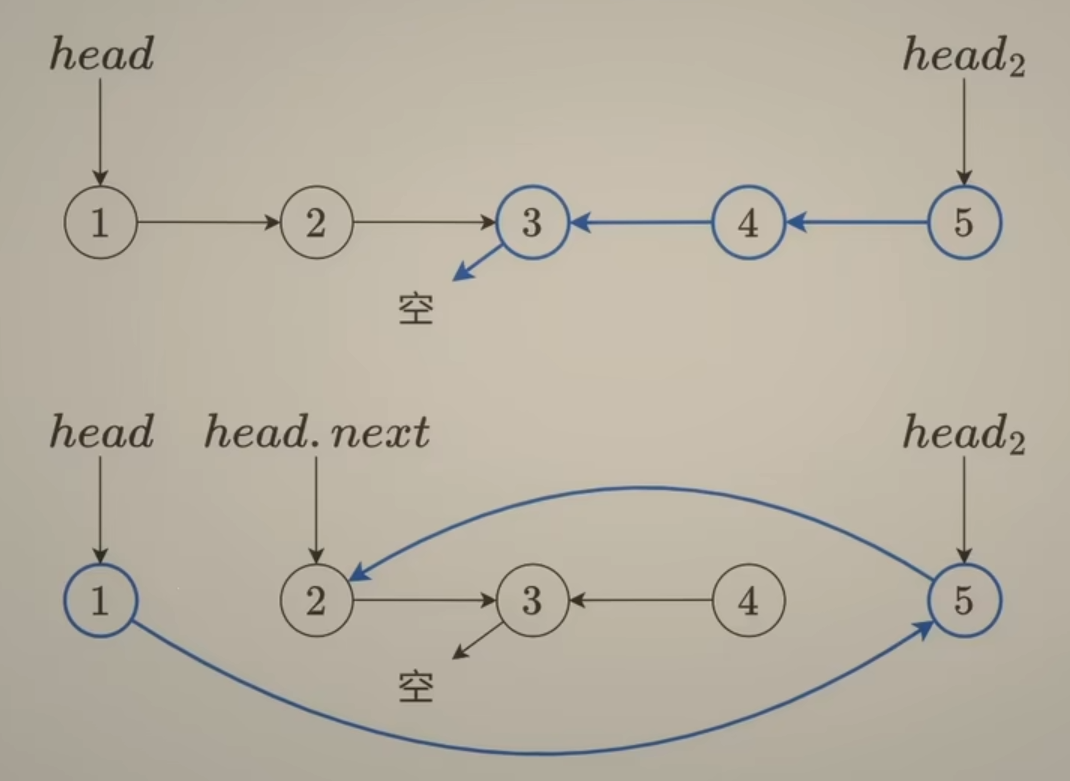
将右边链表的头结点 称为 head2,如何合并?每次循环的时候,先用p = head->next 保存head的next指针,接着修改指针指向:head->next = head2; q = head2->next; head2->next = p;
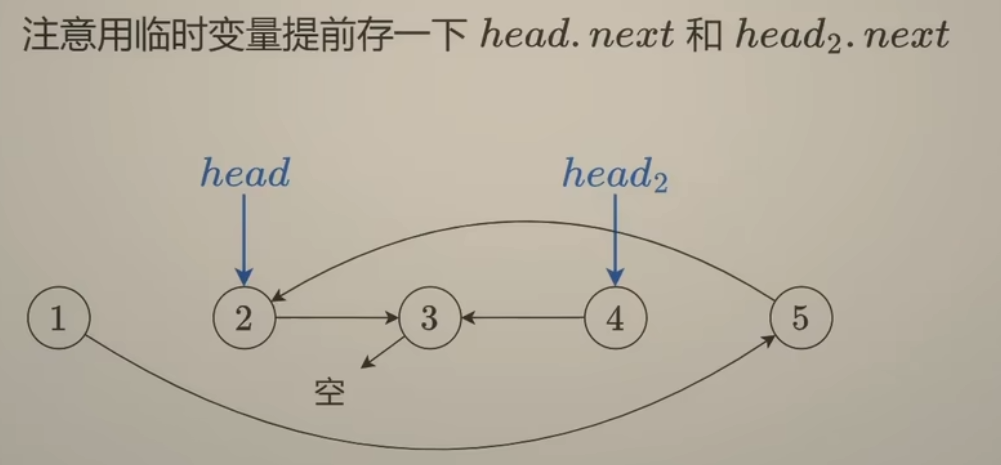
如此不断循环,知道 head2 指向 结点3,或者 head2->next = nullptr,就可以退出循环。
梳理一下整个流程大概如下:
- 找到链表中间结点 mid
- 将 链表后半段 进行反转
- 按照顺序重排指针
复杂度分析:
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
// 重排链表思路如下:
void reorderList(ListNode* head) {
ListNode *fast = head, *slow = head;
// 1. 快慢指针 找到中间结点 slow
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
}
// 2. 反转后半段 链表
ListNode *pre = nullptr;
ListNode *cur = slow, *nxt = nullptr;
while(cur){
nxt = cur->next;
cur->next = pre;
pre = cur;
cur = nxt;
}
// 3. 循环迭代 每次修改head->next 指针 和 head2->next 指针
ListNode *head2 = pre, *p = nullptr, *q = nullptr;
while(head2->next){
p = head->next; // 暂存 head下一个结点
head->next = head2; // 第一次重排
q = head2->next; // 暂存 head2下一个结点
head2->next = p; // 第二次重排
head = p, head2 = q; // head 和 head2 指向原来的next结点
}
}
};
|
课后作业
234. 回文链表
08 前后指针 链表删除 链表去重
单链表删除结点整体思路:
对于单链表来说,要想删除其中的结点,需要利用其 上一个结点,也就是pre结点,做法:把上一个结点指向要删除结点的 下一个结点。如下图:
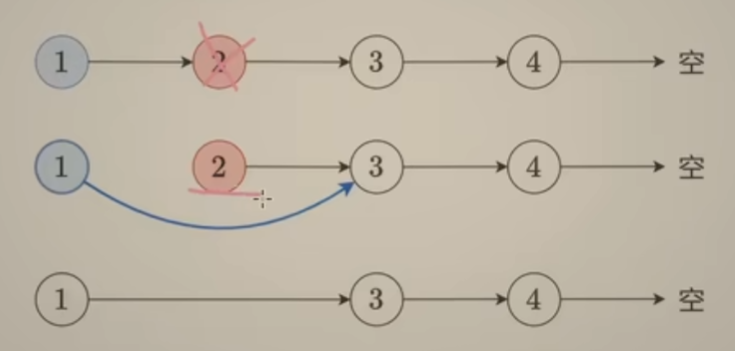
注意:这个 “被删除结点"还是存在的,如果语言自带垃圾回收机制,那它会帮你回收这部分内存,如果是C++可以手动回收,避免内存泄漏。
237. 删除链表中的节点
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
class Solution {
public:
// 注意:要先 用node下一个结点 val 替换 当前 node的val,再进行指针操作
// 否则,可能后面 while循环条件原因,样例:
// [4,5,1,9] 1
// 无法通过测试
void deleteNode(ListNode* node) {
ListNode* p = node->next;
// 定义 指针p指向 node指针的下一个结点
// 最后删除一个结点的时候,p指向最后一个结点,node指向末尾第二个结点
// 直接将 node的next指针指向空,即为删除一个结点
node->val = p->val;
while(p->next){
node = p, p = p->next;
node->val = p->val;
}
node->next = nullptr;
}
};
|
19. 删除链表的倒数第 N 个结点
代码思路:
首先遍历一遍链表 求出长度len,题目要求即为 删除索引为 len-n+1的结点(索引从1开始),需要先找到 索引为 len-n的结点 修改其next指针,从而达到 删除结点。
**注意:**为了保证操作一致性,需要 在head结点之前 申请一个first结点
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
// 思路:首先遍历一遍链表 求出长度len,题目要求即为 删除索引为 len-n+1的结点(索引从1开始)
// 需要先找到 索引为 len-n的结点 修改其next指针,从而达到 删除结点
// 注意:为了保证操作一致性,需要 在head结点之前 申请一个first结点
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *first = new ListNode(0, head);
ListNode *pre = first, *cur = head;
int len = 0;
while(cur){
len++;
cur = cur->next;
}
int index = len - n + 1;
for(int i = 0; i < index-1; ++i)
pre = pre->next;
cur = pre->next;
pre->next = cur->next;
delete cur;
return first->next;
}
};
|
83. 删除排序链表中的重复元素
代码思路:
略。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
ListNode *p = head, *q = nullptr;
while(p){
if(p->next && p->next->val == p->val){
while(p->next && p->next->val == p->val)
q = p->next, p->next = q->next, delete q;
}
p = p->next;
}
return head;
}
};
|
82. 删除排序链表中的重复元素 II
代码思路:
略。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
ListNode* p = head, *q = nullptr, *pre = nullptr;
// 技巧:在 head头结点 前面再定义一个 指引结点
ListNode* first = new ListNode(0, head);
// 注意!!! first->next = head
// 技巧:定义pre指针,指向当前 循环结点p 的前一个结点
// 这样就还可以 在遇到重复元素的结点p的时候,修改pre->next指针,删除p结点
pre = first;
while(p) {
if(p->next && p->next->val == p->val){
// 出现重复数字结点,只保留当前第一个重复数字结点
while(p->next && p->next->val == p->val)
q = p->next, p->next = q->next, delete q;
// 剔除 重复数字的 唯一结点
pre->next = p->next;
delete p;
p = pre->next;
} else{
pre = p;
p = p->next;
}
}
return first->next;
}
};
|
课后作业
203. 移除链表元素
09 二叉树 递归 数学归纳法 栈
如何思考递归?为什么需要使用递归?为什么递归是对的?计算机是怎么执行递归过程的?
二叉树与递归问题思考:

-
如何思考二叉树相关问题:

-
为什么需要使用递归?

执行同一份代码,循环与递归的差异:
- 循环:可以在循环内部 操作循环外部的变量。每次操作的都是同一个变量
- 递归:问题之间是有嵌套关系的,需要把计算结果返回给 上一级问题做计算。
事实上,动态规划也是递归的一种。把原问题拆分成子问题,然后拆分到最后子问题答案显而易见,就得到了整个问题的解。

在上述问题中,递归的边界条件就是空结点,直接返回0作为空结点树的深度。返回的过程就是递归中的归。
-
想清楚上面问题使用递归解决是对的
递归问题:边界条件情况怎么计算,非边界条件情况怎么计算都想清楚了。现在需要证明正确性:
数学归纳法:
- 命题中最基本的情况——边界条件处理
- 命题中相邻规模情况之间的联系——非边界条件处理
=> 从上边两个条件,可以推出最终的结论是对的
-
计算机如何执行递归?
递归每次计算之后,需要把 计算结果返回给它的父节点,此时要知道此时结点的父节点是谁,那就需要提前将父节点的信息保存起来。==要知道返回给谁==是需要一个数据结构的,这个数据结构有个特点就是 “后进先出”,也就是 栈。
最坏情况下,二叉树只有左儿子没有右儿子,那这课二叉树就变成一个链状结构。那这个情况下,栈的大小就会达到O(n),因此空间复杂度为O(n)。
-
另一种递归思路:
在递归过程中,除了把结点传下去,还可以把路径上的结点传下去。在递归过程中,还可以维护一个全局变量,每次路径上结点+1之后,就更新全局变量的最大值。遍历完整颗树,这个全局变量就是答案了。
104. 二叉树的最大深度
最大深度定义:根节点到最远叶子结点的最长路径上的节点数。
完整代码:
递归思路一:
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int maxDepth(TreeNode* root) {
// 边界条件
if(root == nullptr) return 0;
// 递归计算左子树的最大深度
int leftDepth = maxDepth(root->left) + 1;
// 递归计算右子树的最大深度
int rightDepth = maxDepth(root->right) + 1;
return max(leftDepth, rightDepth); // 最后返回二者的最大值
}
};
|
递归思路二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int maxDepth(TreeNode* root) {
int ans = 0;
std::function<void(TreeNode*, int)> func = [&] (TreeNode* root, int cnt) {
if (root == nullptr)
return;
cnt += 1;
ans = max(ans, cnt);
func(root->left, cnt);
func(root->right, cnt);
};
func(root, 0);
return ans;
}
};
|
时间复杂度:O(n)
空间复杂度:O(n)
课后作业
111. 二叉树的最小深度
112. 路径总和
113. 路径总和 II
129. 求根节点到叶节点数字之和
257. 二叉树的所有路径
1448. 统计二叉树中好节点的数目
10 二叉树 相同 对称 平衡 右视图
前一小节讲了解决二叉树问题的两种递归思路,但要灵活运用递归,还需要通过做题目来打开思路。
100. 相同的树
解题思路:
定义相同:对于两棵二叉树,根结点val相同,并且左右子树相同。
- 这样原问题就可以拆分为两个子问题(两棵子树是否相同)来进行判断—非边界条件
- 两棵子树有一棵是 空的,无法继续递归下去,如果两个结点都为空就返回
true,否则就返回false—边界条件
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr || q == nullptr)
return p == q; // 同时结点都为空,返回true;否则,返回false
return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
|
时间复杂度:O(n)
空间复杂度:O(n)
101. 对称二叉树
解题思路:
根结点已经对称,不用管。此时需要看左子树和右子树是否是对称的,注意==这里将左右子树==看作是两棵独立的树,那这样就转换为上述比较两棵树是否"一样"的问题了,不过这里是判断两棵树是否堆成,将递归条件修改一下就可以了。
- 递归比较 左边的左子树和 右边的右子树,看它们是否对称
- 递归比较 左边的右子树和 右边的左子树,看它们是否对称
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
bool isSymmetric(TreeNode* root) {
// Variable 'isSymmetric' cannot be implicitly captured in a lambda with no capture-default specified
// [] 不能在Lambda中隐式获取 with 没有默认获取标识符
// 使用 [=] 传值会有警告:Variable 'isReflect' is uninitialized when used within its own initialization
// 并且提交上去会报错
std::function<bool(TreeNode*, TreeNode*)> isReflect = [&](TreeNode *p, TreeNode *q) {
if(p == nullptr || q == nullptr)
return p == q;
return p->val == q->val && isReflect(p->left, q->right) && isReflect(p->right, q->left);
};
return isReflect(root->left, root->right);
}
};
|
110. 平衡二叉树
解题思路:
高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
参考之前讲的二叉树的最大深度,通过递归得到左右两棵子树的高度。高度有了,算一下高度差绝对值,就可以判断是否为高度平衡二叉树。
思考:若是这棵树不是高度平衡二叉树,返回值设置为什么?
递归调用 求左右子树最大高度的函数返回值设置为 高度height,而``height >= 0`恒成立,若是高度不平衡可以返回一个负数,就可以统一函数的边界情况返回值 和 非边界情况返回值类型了。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
bool isBalanced(TreeNode* root) {
std::function<int(TreeNode*)> get_height = [&] (TreeNode *node) {
if(node == nullptr)
return 0;
int left_height = get_height(node->left);
if(left_height == -1)
return -1;
int right_height = get_height(node->right);
if(right_height == -1)
return -1;
// 判断左右子树 高度差是否大于1,如果是整棵树不平衡,返回-1;否则,返回两棵子树最大高度+1
return abs(left_height-right_height)>1 ? -1 : max(left_height, right_height)+1;
};
int ans = get_height(root);
// 这里可以简写为 ans != -1
return ans == -1 ? false : true;
}
};
|
199. 二叉树的右视图
解题思路:
可以先 递归右子树,再递归左子树。两个问题:
- 怎么把答案记下来
- 怎么判断这个结点是否需要记录到答案中
可以用到前一节讲的一个方法:==在递归的同时记录一个节点个数== 或者 递归深度,如果递归深度等于答案长度 那么这个节点就需要记录到答案中。这句话要怎么理解呢?下面举一个简单例子来说明:
- 答案初始为空,长度也为0,把根结点 记录
- 继续递归,深度为1,答案长度也为1,记录当前节点
以此类推。这个利用 右视图中相同高度的节点会 遮挡后边节点原理 这个技巧来完成的。
思路二:层序遍历,取每一层的最后一个节点。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> ans;
std::function<void(TreeNode*, int)> func = [&] (TreeNode *node, int depth) {
if(node == nullptr)
return;
if(depth == ans.size())
ans.push_back(node->val);
func(node->right, depth+1);
func(node->left, depth+1);
};
func(root, 0);
return ans;
}
};
|
课后作业
226.翻转二叉树
1026.节点与其祖先之间的最大差值
1080.根到叶路径上的不足节点
1110.删点成林
1372.二叉树中的最长交错路径
11 二叉搜索树 前序 中序 后序
98.验证二叉搜索树
解题思路:
这道题三种解题思路:

二叉搜索树定义:对于一个节点来说,它的左子树所有节点值都小于 它的值,右子树所有节点值都大于 它的值。同时它的 左右子树都是二叉搜索树。
用不同的角度去看这个定义,就会得到不同的方法:
-
方法一:观察下边每个节点都有一个对应的区间范围,在这个范围中,对节点元素进行判断,符合要求即为二叉搜索树。
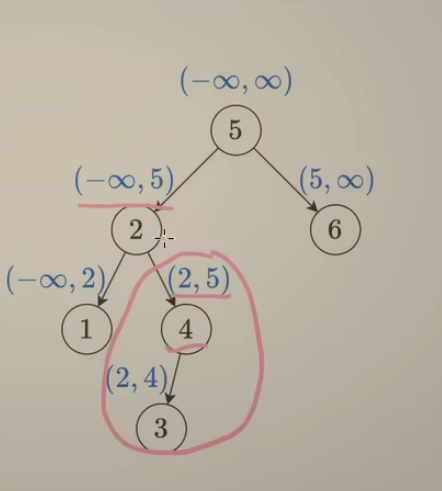
使用递归实现,递归的时候,除了传入节点,还需要传入这个开区间的范围
- 对于每个节点,先判断它的节点值 是否在开区间内,然后往下进行递归
- 往左边递归,把开区间的右边界更新为节点值
- 往右边递归,把开区间的左边界更新为节点值
注意:对于根结点,函数入口,没有父节点,把区间范围更新为(-$\infin$ , +$\infin$ )
-
方法二:中序遍历所有节点,理论上可以得到一个 严格递增的数组。如果不是二叉搜索树,则不是一个递增数组。
在遍历过程中记录上一个节点值,比较当前节点值 是否 大于上一个遍历的节点值,如果全部节点值都符合这个规律,则为二叉搜索树。
-
方法三:后序遍历,将 节点值的范围往上传递,比如:对于 根结点5来说,5大于左子树传上来范围的最大值4,小于右子树传上来范围的最小值6,那么这棵树就符合二叉搜索树的定义。
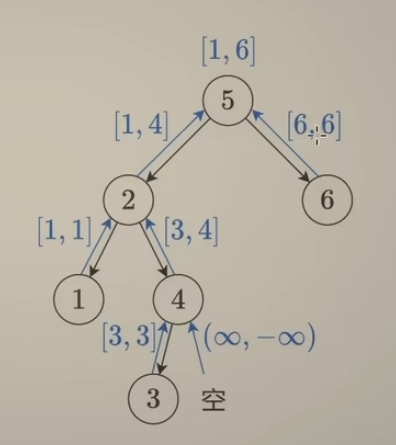
看上去,似乎左子树只需要返回 给父节点一个最大值,右子树只需要返回 给父节点一个最小值就行了,但是这样不对,例如:将下边的节点4 改为 节点值6,若是值传右子树最小值3,那么就无法比较 根结点值5 和 节点值6的大小了,会出现判断失误,如下:
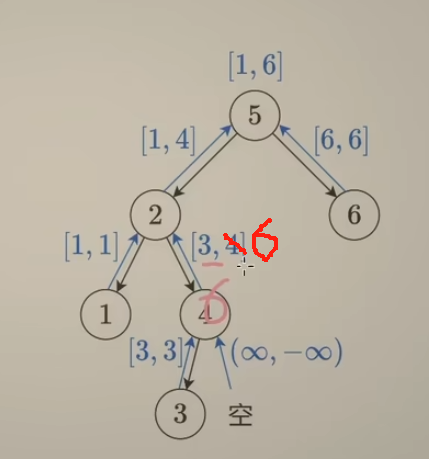
为了简化代码逻辑,递归到空结点,这种情况可以返回范围 ($\infin$ , -$\infin$ ),另外中途发现不是一棵二叉搜索树,可以额外返回一个 Flase,或者返回 负无穷到正无穷(这个可以保证 x <= l_max or x >= r_min 这个条件本身不成立。然后每次 递归到最后,返回的是 min(l_min, x), max(r_max, x) 这个为何要 x参与比较,因为一开始空结点的时候,返回的是inf, -inf,使用x参与比较可以把空结点返回值给剔除掉。
这个题解比较巧妙,需要每次返回一个 pair<int, int>对象(如果使用C++写的话),下边提供一个UP给的python代码,来理解题目:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def f(node):
if node is None:
return inf, -inf
l_min, l_max = f(node.left)
r_min, r_max = f(node.right)
x = node.val
if x <= l_max or x >= r_min: # 这棵树不是二叉搜索树,退出,可以发现下边这个二元组返回的 范围,可以保证 x <= l_max or x >= l_min 这个条件本身不成立,
#而且 还可以巧妙地发现 在后边符合条件返回 min(l_min, x), max(r_max, x)的时候,还是返回-inf, inf
# 这样 如果某个节点已经 判断出不是一棵二叉搜索树,那么其最后返回到根结点的二元组还是(-inf, inf)
return -inf, inf
return min(l_min, x), max( r_max, x)
return f(root)[1] != inf # 这里 如果 返回的最大值为 inf,说明这不是一棵二叉搜索树
|
复杂度分析:
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class Solution {
public:
// 法一:前序遍历 将节点值传递给子树 进行二叉搜索树判定
bool isValidBST(TreeNode* root) {
unsigned int inf = 2.7e9; // 范围已经超出 2^31 ,如果赋值给 int类型,并且添加符号想着得到负无穷
// 最后 int类型由于 负数下溢出 会转换为 正数...
const long long infinit = 0x3f3f3f3f3f3f3f3f;
std::function<bool(TreeNode*, long long , long long)> isValid = [&] (TreeNode *root, long long left, long long right) {
if(root == nullptr)
return true;
int val = root->val;
return (val < right && val > left) && isValid(root->left, left, val) && isValid(root->right, val, right);
};
long long l = -infinit, r = infinit; // 这里应该 left 为 负无穷,一开始传入成正无穷 样例过不了还检查半天
// 第一次传入 left, right使用默认的 infinit即可
return isValid(root, l, r);
}
// 法二:中序遍历,检查每个相邻节点值 是否 遵循严格递增顺序
bool isValidBST1(TreeNode* root) {
// 由于 -2^31 <= Node.val <= 2^31 - 1
// 正无穷 和 负无穷 得使用比 int 数值范围大的数来赋值
const long long infinit = 0x3f3f3f3f3f3f3f3f;
long long pre = -infinit;
std::function<bool(TreeNode*)> isValid = [&](TreeNode *node) {
if(node == nullptr)
return true;
if(!isValid(node->left))
return false;
if(node->val <= pre)
return false;
pre = node->val; // 更新节点值
return isValid(node->right);
};
return isValid(root);
}
// 前面 前序遍历 是把节点值范围 往下传
// 还可以把节点值的范围 往上传
// 法三:后序遍历 将节点值传递到父节点
// 执行用时:击败97.80% 使用 C++ 的用户
bool isValidBST2(TreeNode* root) {
const long long infinit = 0x3f3f3f3f3f3f3f3f;
std::function<pair<long long, long long>(TreeNode*)> isValid = [&](TreeNode *node) {
if(node == nullptr)
return make_pair(infinit, -infinit);
pair<long long, long long> ret = isValid(node->left);
long long l_min = ret.first, l_max = ret.second;
ret = isValid(node->right);
long long r_min = ret.first, r_max = ret.second;
long long x = node->val;
if(x <= l_max || x >= r_min)
return make_pair(-infinit, infinit);
return make_pair(min(l_min, x), max(r_max, x));
};
return isValid(root).second != infinit;
}
};
|
课后作业
203.二叉搜索树中第K小的元素
501.二叉搜索树中的众数
530.二叉搜索树的最小绝对差
700.二叉搜索树中的搜索
1373.二叉搜索子树的最大键值和
12 二叉树 最近公共祖先
最近公共祖先定义:对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)
236.二叉树的最近公共祖先
解题思路:
分类讨论如下

-
当前节点是空节点:直接返回即可
-
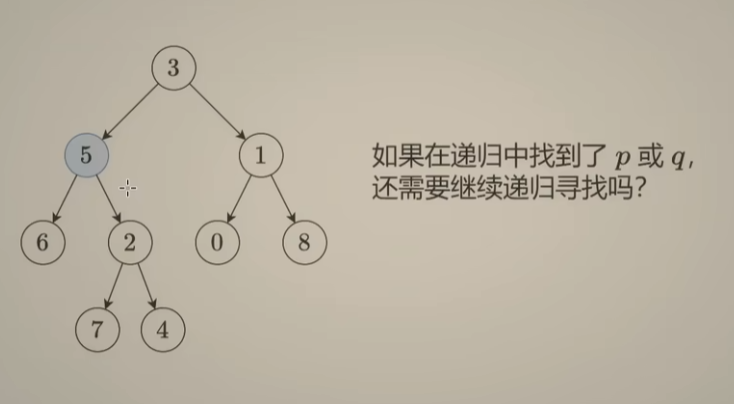
当前节点是 p 或 q:不需要递归寻找,返回 p 或 q即可(注意:返回p 或 q不代表最终答案为 p/q的值)。假设此时的节点p:
- 当节点q在节点p的子树中时,不需要递归,节点p就是其所求的公共祖先;
- 当节点q不在节点p的子树中时,也不需要递归,应该遍历根结点的其他子树
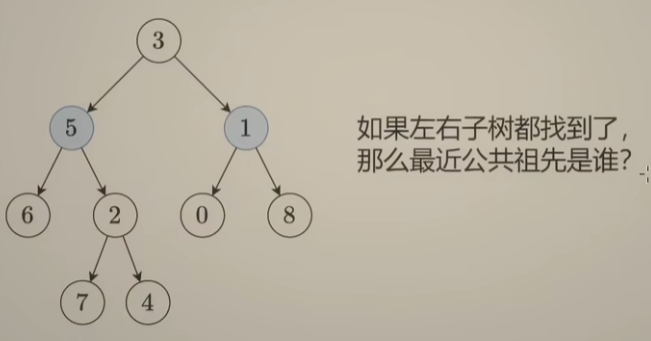
-
如果左右子树都找到了?最近公共祖先就是当前结点,例如下边的 结点3:
-
如果左子树找到了,右子树没有,返回递归左子树后的结果即可
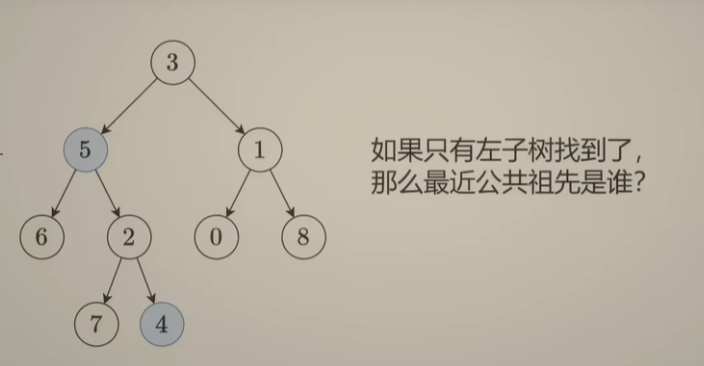
分类讨论最终结果如下:

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr || root == p || root == q)
return root;
TreeNode* left, *right;
left = lowestCommonAncestor(root->left, p, q);
right = lowestCommonAncestor(root->right, p, q);
if(left && right)
return root;
// if(left != nullptr && right == nullptr)
// return left;
// if(left == nullptr && right != nullptr)
// return right;
// return nullptr;
// 上边逻辑简写如下:
if(left)
return left;
else
return right;
}
};
|
时间复杂度:O(n)
空间复杂度:O(n)
235.二叉搜索树的最近公共祖先
解题思路:
利用二叉搜索树的性质来解最近公共祖先。
当前节点值val与p->val和 q->val 比较:
- 情况一
val > p->val && val < q->val:p和q在两颗子树中,返回当前节点
- 情况二
val == p->val || val == q->val:当前节点为p或者q,返回当前节点
- 情况三
val > p->val && val > q->val:p和q都在左子树中,返回递归左子树的结果,最终归结为情况2
- 情况四
val < p-val && val < q->val:p和q都在右子树中,返回递归右子树的结果,最终归结为情况2

思考:当前节点是空节点,是否需要判断?
题目保证p和q都在这棵树中,那么根节点不是空节点,如果都在左边,左子树非空;如果都在右边,右子树非空;对于其他情况,p和q都在两侧或者当前节点是p或q,当前节点都不是空节点。所以不需要判断当前节点是否为空节点。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
int val = root->val;
// 1. p和q都在左子树
if(val > p->val && val > q->val)
return lowestCommonAncestor(root->left, p, q);
// 2. p和q都在右子树
if(val < p->val && val < q->val)
return lowestCommonAncestor(root->right, p, q);
// 3. p和q在左右子树 或者 当前节点就为p或q
return root;
}
};
|
时间复杂度:O(n)
空间复杂度:O(n)
课后作业
1123.最深叶节点的最近公共祖先
2096.二叉树一个节点到另一个节点每一步的方向
13 二叉树 层序遍历 BFS 队列
102.二叉树的层序遍历
解题思路:
之前将的递归是从根结点出发,径直地往下走,是深度优先搜索。而层序遍历是一行一行遍历:
法一:双数组模拟层序遍历
时间复杂度:由于每个节点都会遍历一次,所以复杂度为O(n)
空间复杂度:由于在满二叉树中,最后一层大约会有 n/2个节点,空间复杂度为O(n)
法二:尝试使用一个数组解决上边的问题(队列)
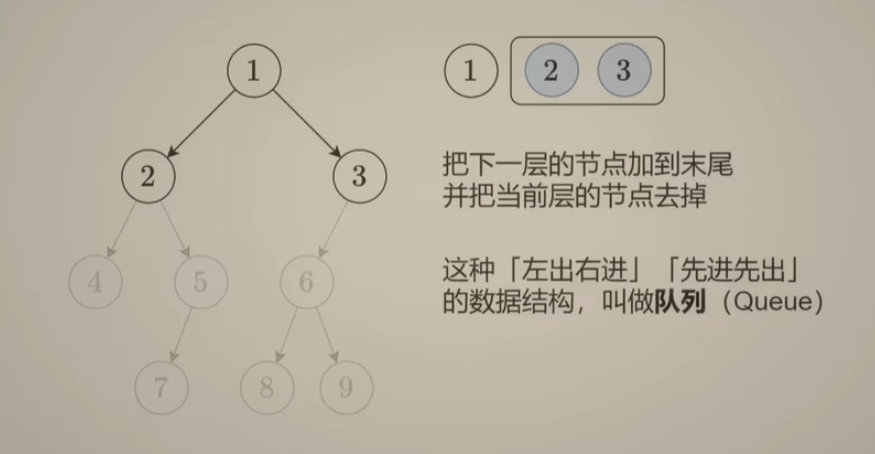
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
class Solution {
public:
// 法一:使用 cur数组 和 nxt数组模拟队列
// 执行用时:击败 86.71% 使用 C++ 的用户
// 消耗内存分布:击败 11.26% 使用 C++ 的用户
vector<vector<int>> levelOrder(TreeNode* root) {
if(root == nullptr)
return {};
vector<vector<int>> ans;
vector<TreeNode*> cur(1, root), nxt;
vector<int> vals;
while(!cur.empty()) {
for(int i = 0; i < cur.size(); ++i){
if(cur[i]->left)
nxt.push_back(cur[i]->left);
if(cur[i]->right)
nxt.push_back(cur[i]->right);
vals.push_back(cur[i]->val);
}
ans.push_back(vals);
vals = {};
cur = nxt;
nxt = {};
}
return ans;
}
// 法二:使用队列容器
// 执行:击败 51.62% 使用 C++ 的用户
// 消耗内存分布: 击败 8.86% C++ 的用户
vector<vector<int>> levelOrder1(TreeNode* root) {
if(root == nullptr)
return {};
vector<vector<int>> ans;
queue<TreeNode*> qt; qt.push(root);
TreeNode *tmp;
while(!qt.empty()) {
vector<int> vals;
int len = qt.size();
for (int i = 0; i < len; ++i){
tmp = qt.front(); qt.pop();
vals.push_back(tmp->val);
if(tmp->left) qt.push(tmp->left);
if(tmp->right) qt.push(tmp->right);
}
ans.push_back(vals);
}
return ans;
}
};
|
小结:之前做的 《求二叉树最大深度》也可以使用层序遍历来做,这个最大深度指的是上边的 ans 数组长度。比较一下层序遍历和递归,计算机在实现递归会用一个栈来维护入栈出栈过程,代码简洁;而层序遍历需要自己手动编写 入队出队的代码。相比于递归写法,层序遍历代码就没那么简洁了。
103.二叉树的锯齿形层序遍历
解题思路:
类比102题,唯一不同就是需要将 偶数层的数组元素翻转一下再添加到结果数组中
- 法一:利用 栈来翻转偶数层数组元素
- 法二:直接搞多一个数组,将偶数层正序元素翻转一下即可
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
class Solution {
public:
// 下边的代码有问题:通过不了这个测试样例 root = [1,2,3,4,null,null,5]
// 实际输出:[[1],[3,2],[5,4]] 预期结果:[[1],[3,2],[4,5]]
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
// 需要特判一下 root == nullptr直接返回 ,否则后边:vals.push_back(tmp->val); 指针root访问val出错
if(root == nullptr)
return {};
vector<vector<int>> ans;
queue<TreeNode*> qt;
qt.push(root);
TreeNode *tmp;
bool layer = false; // true 代表偶数层 从右向左扫描入队节点; false 代表奇数层 从左往右扫描入队节点
while(!qt.empty()) {
layer = !layer;
vector<int> vals;
int len = qt.size();
for(int i = 0; i < len; ++i){
tmp = qt.front(); qt.pop();
vals.push_back(tmp->val);
if(layer){
if(tmp->right) qt.push(tmp->right);
if(tmp->left) qt.push(tmp->left);
}else{
if(tmp->left) qt.push(tmp->left);
if(tmp->right) qt.push(tmp->right);
}
}
ans.push_back(vals);
}
return ans;
}
// 法一:利用栈来反转 偶数层的数组元素
// 正常层序遍历,不过返回值 需要呈现 每一层 节点值顺序不同
// - 奇数层:正常出队,正常把 节点val添加到层次 数组中
// - 偶数层:正常出队,把出队节点入栈先,等到整层都遍历完之后,再将栈中 节点val添加到层次 数组中
// 执行用时分布:击败 100.00% 使用 C++ 的用户
// 消耗内存分布:击败 9.25% 使用 C++ 的用户
vector<vector<int>> zigzagLevelOrder1(TreeNode* root) {
if(root == nullptr)
return {};
vector<vector<int>> ans;
queue<TreeNode*> qt;
stack<TreeNode*> st;
qt.push(root);
TreeNode *tmp;
bool layer = true; // false 奇数层取数; true 偶数层取数
// 这里意义 一开始已经取完第0层节点值,接下来循环开始从第1层开始取节点值
while(!qt.empty()){
layer = !layer;
vector<int> vals;
int len = qt.size();
for(int i = 0; i < len; ++i){
tmp = qt.front(); qt.pop();
if(tmp->left) qt.push(tmp->left);
if(tmp->right) qt.push(tmp->right);
if(!layer){
vals.push_back(tmp->val);
}else{
st.push(tmp);
}
}
if(!layer){
ans.push_back(vals);
continue;
}
while(!st.empty()){
tmp = st.top(); st.pop();
vals.push_back(tmp->val);
}
ans.push_back(vals);
}
return ans;
}
};
|
// 法二:直接构造多一个数组,将偶数层的数组元素反转即可,下边参照博主代码,使用python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
cur = [root]
even = False
while cur:
next = []
vals = []
for node in cur:
vals.append(node.val)
if node.left: nxt.append(node.left)
if node.right: nxt.append(node.right)
cur = nxt
ans.append(vals[::-1] if even else vals)
even = not even
return ans
|
513.找树左下角的值
代码思路:
- 法一:返回最后一层的第一个节点
- 法二:把层序遍历改成 从右到左遍历,最后一个节点就是最底层最左边的节点了
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
class Solution {
public:
// 法一:返回最后一层的第一个节点
// 使用层序遍历即可
int findBottomLeftValue(TreeNode* root) {
vector<vector<int>> ans;
vector<TreeNode*> cur(1, root), nxt;
vector<int> vals;
while(!cur.empty()) {
for(int i = 0; i < cur.size(); ++i){
if(cur[i]->left)
nxt.push_back(cur[i]->left);
if(cur[i]->right)
nxt.push_back(cur[i]->right);
vals.push_back(cur[i]->val);
}
ans.push_back(vals);
vals = {};
cur = nxt;
nxt = {};
}
vals = ans[ans.size()-1];
return vals[0];
}
// 法二:把层序遍历改成 从右到左遍历,最后一个节点就是最底层最左边的节点了
// 从右到左遍历,改变一下节点的入队顺序即可
int findBottomLeftValue1(TreeNode* root) {
queue<TreeNode*> qt; qt.push(root);
TreeNode *tmp;
while(!qt.empty()) {
vector<int> vals;
int len = qt.size();
for (int i = 0; i < len; ++i){
tmp = qt.front(); qt.pop();
vals.push_back(tmp->val);
if(tmp->right) qt.push(tmp->right);
if(tmp->left) qt.push(tmp->left);
}
if(qt.empty())
return tmp->val;
}
// 判题机对于有返回值的函数 有明显返回值的情况会报错
// 不过这一题保证了一定有返回值
return root->val;
}
// 执行用时分布:击败7.08% 使用 C++ 的用户
// 消耗内存分布:击败 97.70% 使用 C++ 的用户
// 上边代码可以简化如下:
int findBottomLeftValue2(TreeNode* root) {
queue<TreeNode*> qt; qt.push(root);
TreeNode *tmp;
while(!qt.empty()) {
tmp = qt.front(); qt.pop();
if(tmp->right) qt.push(tmp->right);
if(tmp->left) qt.push(tmp->left);
}
// 返回最后一个节点的值即可
return tmp->val;
}
};
|
课后作业
104.二叉树的最大深度
111.二叉树的最小深度
199.二叉树的右视图
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针 II
1302.层数最深叶子节点的和
1609.奇偶树
2415.反转二叉树的奇数层
2641.二叉树的堂兄弟节点 II
14 回溯 子集型 分割回文串
回溯问题讲解
- 回溯概念
- 回溯三问:思考回溯问题的套路
- 子集型回溯—回溯问题一种类型
-
单纯的循环嵌套,表达能力有局限

-
思考:原问题和子问题,可以使用递归解决,通过递归可以达到多重循环的效果

-
回溯:有一个增量构造答案的过程,这个过程通常可以使用递归实现
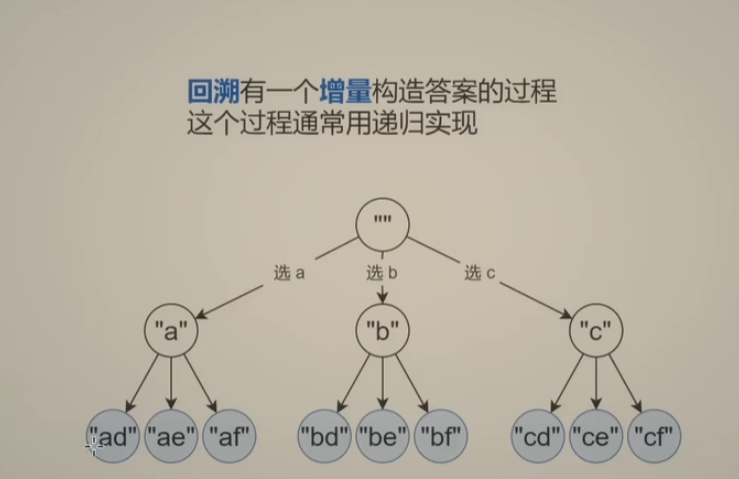
-
递归写法关键:处理好 边界条件和非边界条件逻辑即可,其他事情可以交给数学归纳法。思考递归,重点思考如何推导两个相邻问题和子问题之间的转换—非边界条件逻辑,如下:
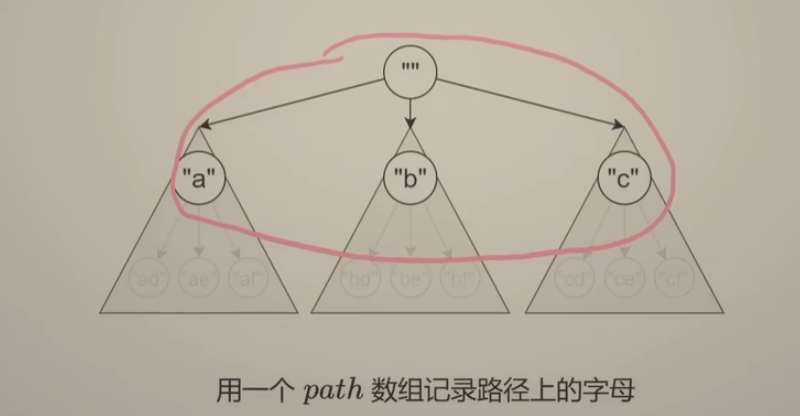
回溯三问: 思考回溯问题 和 动态规划问题的模板

首先把要把数字和要枚举的字母对应起来,使用数组。
回溯问题分类:
- 子集型回溯(0-1背包问题也可以算作一种子集型回溯)
- 组合型回溯
- 排列型回溯
小结:
- 子集型回溯 和 组合型回溯解题方法:
- 选当前元素 或者 不选—输入视角
- 枚举选哪个,选举的集合都是一个答案—答案视角
- 注:有的题目适合用 第一种做法(比如:22.括号生成),有的题目更适合用 枚举选哪个思路来解题(比如:131.分割回文串),平时做题的时候,两种方法都可以考虑,比较哪一种比较好写就使用哪一种思路来写即可
17.电话号码的字母组合
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
class Solution {
private:
// 这个一开始 设置为numToStr[10] 导致后边访问
string numToStr[9] = {"", "abc", "def", "ghi", "jkl", "mno", "pqrs",
"tuv", "wxyz"};
public:
// 下面这种做法,由于 tmp是一个局部变量,无法在多个函数之间进行传递值?反正跑出来结果是这样的
vector<string> letterCombinations(string digits) {
vector<string> ans;
int len = digits.length();
std::function<void(int, string)> dfs = [&](int pos, string str) {
if(pos == len){
ans.push_back(str);
return;
}
int size = numToStr[digits[pos]-1].length();
for(int i = 0; i < size; ++i){
string tmp = str;
dfs(pos+1, tmp + numToStr[digits[pos]-1][i]);
}
};
dfs(0, "");
return ans;
}
// 下边这种 path字符串初始化在函数外边 是一个非临时变量(相对于函数来说),结果可以存储到ans中
vector<string> letterCombinations1(string digits) {
vector<string> ans;
int len = digits.length();
if(len == 0) return {};
string path(len, 0); // 初始化 字符串长度为len,每一个字符使用 '0'填充
std::function<void(int)> dfs = [&](int pos) {
if(pos == len){
// ans.push_back(str);
// emplace_back 与 push_back 区别是啥来着..
// ans.push_back(path);
ans.emplace_back(path);
return;
}
// 注意:digits[pos]这里是字符,不是数字,不能直接和1相减,要与'1'相减
// 如果和 1相减 会数组越界
//int size = numToStr[digits[pos]-1].length();
int size = numToStr[digits[pos] - '1'].length();
for(int i = 0; i < size; ++i){
// 下边的numToStr[digits[pos]-1] 没有这个字符串,访问会出现下边错误
// Line 1053: Char 9: runtime error: reference binding to null pointer of type 'char' (basic_string.h)
//SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior /usr/bin/../lib/gcc/x86_64-linux-gnu/11/../../../../include/c++/11/bits/basic_string.h:1062:9
path[pos] = numToStr[digits[pos]-'1'][i];
dfs(pos+1);
}
// 上边使用 循环遍历用下标访问 字符串数组元素,更加优雅是使用C++11 中的迭代循环,这样不用下标访问数组位置
// 可以避免一些报错
// for (char c : MAPPING[digits[i] - '0']) {
// path[i] = c;
// dfs(i + 1);
// }
//
};
dfs(0);
return ans;
}
};
|
灵神写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
MAPPING = "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
n = len(digits)
if n == 0:
return []
ans = []
path = [''] * n
def dfs(i: int) -> None:
if i == n:
ans.append(''.join(path))
return
for c in MAPPING[int(digits[i])]:
path[i] = c
dfs(i + 1)
dfs(0)
return ans
|
**时间复杂度:**对于回溯,看作循环,输入数字长度为n(递归栈深度为n,可以看作n重 循环,最终的每一个字符串长度都为n),数字映射到字符串数组长度最多为4,嵌套遍历每一个字符串用乘法法则计算:$4\times 4 \times…$(总的使用排列组合有$4^n$种情况)
-
[灵神解释:O(n$4^n$),其中 n为 digits 的长度。最坏情况下每次需要枚举 4个字母,递归次数为一个满四叉树的节点个数,那么一共会递归 O(4^n)次(等比数列和),再算上加入答案时需要 O(n) 的时间,所以时间复杂度为 O(n4^n);
-
小疑问:vector中每次添加一个元素都需要O(n)时间复杂度么?
-
GPT回答:在 C++ 的标准库中,std::vector 是一个动态数组实现,它具有自动扩展和收缩的功能。当向 std::vector 添加元素时,如果当前容量不足,会触发重新分配内存的过程。这意味着每次添加元素并触发容量扩展时,都需要将原有的元素复制到新的内存空间中,这个操作的时间复杂度是 O(n),其中 n 是当前 std::vector 的大小]
**空间复杂度:**O(n)
78.子集
解题思路:
-
问题核心:每个元素都可以 选 或 不选

-
站在 输入 的角度:
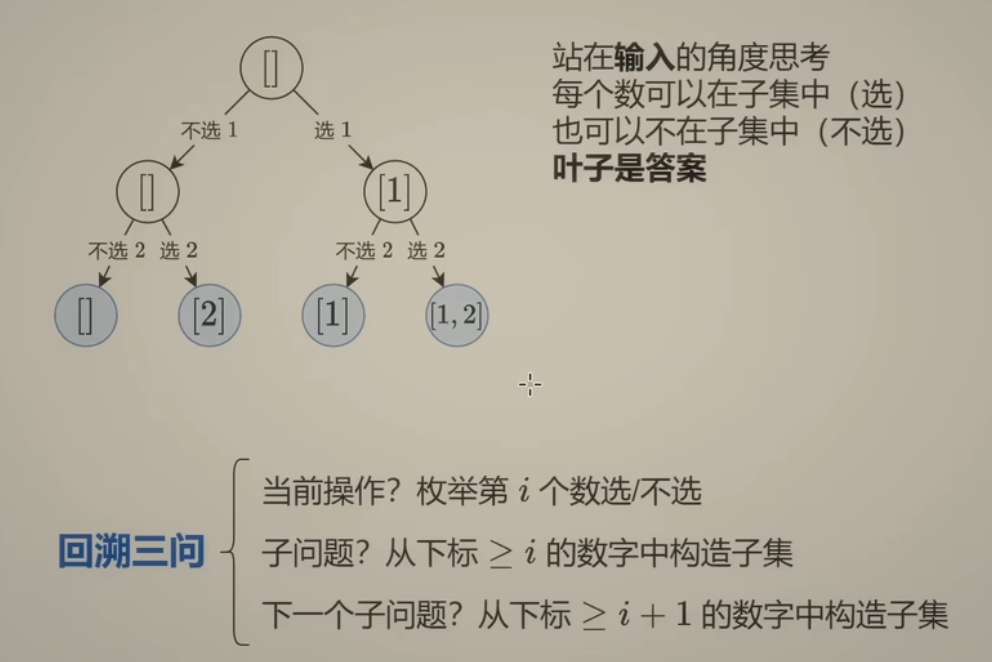
-
站在答案的 视角,每个节点都是答案
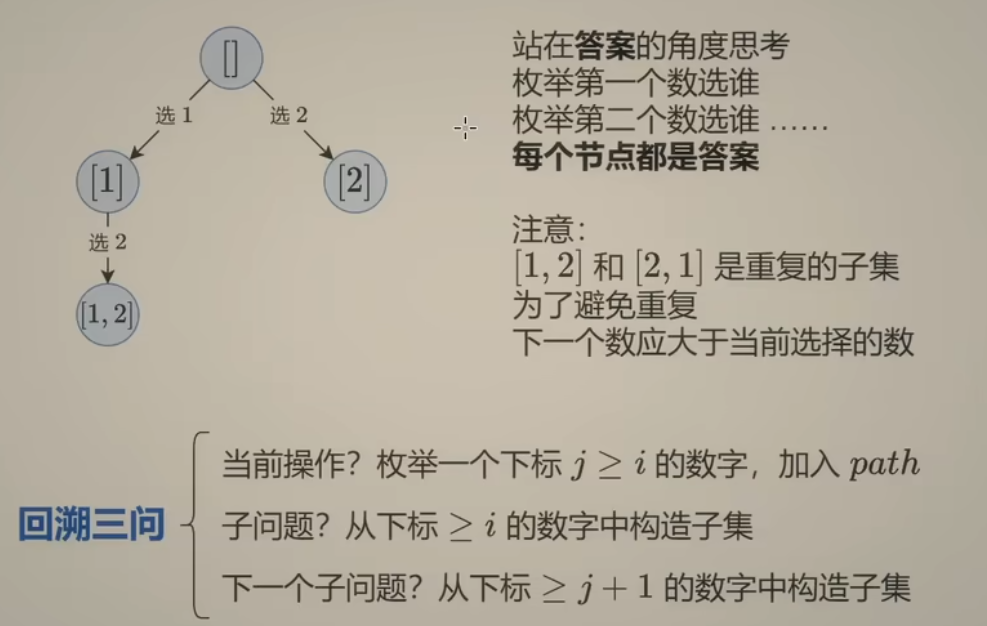
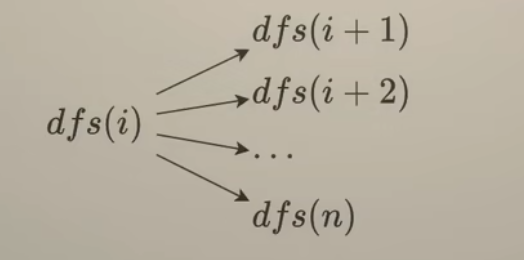
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
public:
// 法一:输入视角, 对于每个数字 选 或 不选
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> ans;
int size = nums.size();
vector<int> path;
function<void(int)> dfs = [&](int i) {
if(i == size){
ans.emplace_back(path);
return;
}
// 不选当前的数字
dfs(i+1);
// 选 nums[i]
path.push_back(nums[i]);
dfs(i+1);
path.pop_back(); // 恢复现场
};
dfs(0);
return ans;
}
// 法二:答案视角,每个节点都是答案,选哪个数
vector<vector<int>> subsets1(vector<int>& nums) {
vector<vector<int>> ans;
vector<int> path;
int n = nums.size();
function<void(int)> dfs = [&] (int i) {
ans.emplace_back(path);
if(i == n) return;
for(int j = i; j < n; ++j){ // 枚举选择数字
path.push_back(nums[j]);
dfs(j+1);
path.pop_back(); // 恢复现场
}
};
dfs(0);
return ans;
}
};
|
时间复杂度:
- 法一输入视角:其中 n 为
nums 的长度。每次都是选或不选,递归次数为一个满二叉树的节点个数,那么一共会递归 O($2^n$) 次(等比数列和),再算上加入答案时需要 O(n) 的时间,所以时间复杂度为 O($n2^n$)
- 法二答案视角:O($n2^n$),其中 n 为 nums 的长度。答案的长度为子集的个数,即 $2^n$,同时每次递归都把一个数组放入答案,因此会递归 $2^n$次,再算上加入答案时需要 O(n)的时间,所以时间复杂度为 O($n2^n$)。
空间复杂度:O(n)
语言收获:
C++中vecotr容器不同函数用法
1
2
3
4
5
|
// 向 容器中添加元素方法(容器尾部添加)
push_back();
emplace_back();
// 将 容器中尾部元素弹出
pop_back()
|
131.分割回文串
解题思路:
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
private:
bool isPlalindrome(string str){
int n = str.size();
int mid = n / 2;
bool flag = true;
for(int i = 0; i <= mid; ++i){
if(str[i] != str[n-1-i]){
flag = false; break;
}
}
return flag;
};
public:
// 站在答案视角 灵神做法
vector<vector<string>> partition(string s){
vector<vector<string>> ans;
vector<string> result;
int n = s.length();
std::function<void(int)> dfs = [&](int i) {
if(i == n){
ans.push_back(result);
return;
}
for(int j = i; j < n; ++j){
string str = s.substr(i, j-i+1);
if(isPlalindrome(str)){
result.push_back(str);
dfs(j+1);
result.pop_back();
}
}
};
dfs(0);
return ans;
}
// 法二:站在输入的视角,选择逗号 or 不选择逗号
};
|
**时间复杂度:**O($n2^n$),其中 n 为 s 的长度。答案的长度至多为逗号子集的个数,即 O($2^n$),因此会递归 O($2^n$) 次,再算上判断回文和加入答案时需要 O(n) 的时间,所以时间复杂度为 O($n2^n$)
**空间复杂度:**O(n)
课后作业
784.字母大小写全排列
1601.最多可达成的换楼请求数目
2397.被列覆盖的最多行数
306.累加数
2698.求一个整数的惩罚数
15 回溯 组合型 剪纸

- 组合型回溯的 解题思路
- 剪枝 技巧
- 分析回溯的 时间复杂度
77. 组合
-
回顾上一讲中的 子集搜索树
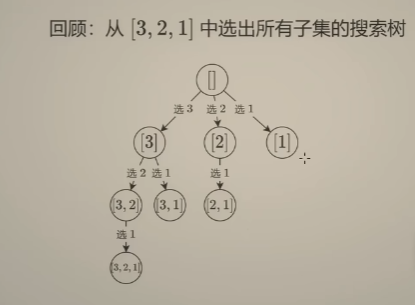
可以看出每一层中,节点中的数字个数是相等的。恰好可以表示集合中选择 1个数的三种情况、2个数的三种情况以及 选择3个数的一种情况(关键在于选择数的时候遵循 数字大小顺序,不会造成集合重复)——这恰好是组合问题
-
在 子集搜索树的基础上添加一个限制:选择n个数对应的路径长度也为 n
从n个数中选 k个数的组合,可以看成是长度固定的子集
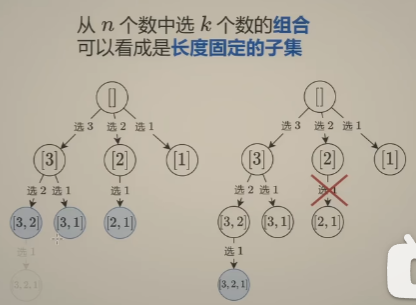
-
剪枝优化组合问题

上面情况是倒序枚举,正序枚举即是 从[i, n]这 n - i + 1个数中选出d个数,若是 n - i + 1 < d,最后无法选出k个数,也可以提前剪枝
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
// 法一:答案视角,每个节点都是答案,选哪个数
vector<vector<int>> combine(int n, int k) {
vector<vector<int>> ans;
vector<int> path;
std::function<void(int)> dfs = [&](int i) {
int d = k - path.size(); // 剩下需要枚举的 数字个数
if(i < d) return; // 剪枝
if(path.size() == k){
ans.push_back(path);
return;
}
// 上边的剪枝也可以隐含 写在循环中
// for(int j = i; j >= d-1; j--)
for(int j = i; j >= 1; j--){
path.push_back(j); // 合法数字范围 [1, n]
dfs(j - 1);
path.pop_back();
}
};
dfs(n); // 逆序枚举
return ans;
}
// 法二:输入视角,对于每个数字 选 或 不选
};
|
**时间复杂度分析:**分析回溯问题的时间复杂度,有一个通用公式:路径长度×搜索树的叶子数。对于本题,它等于 O(k⋅C(n,k))。
**空间复杂度:**O(k)
216. 组合总和 III
代码思路:
类似上一题,只不过上一题是从[1, n]中选择所有可能的k个数的组合;这一题要求改为 数字只能在[1, 9]中选取,且只选取 k个数组合 相加之后的和为n的

完整代码: 这里我的思路是从1开始枚举到9,然后利用参数 nums计算集合元素个数,使用sum计算集合元素之和是否达到n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
// 法一:答案视角,每个节点中 数字的集合都是答案,关键在于答案是否符合要求
vector<vector<int>> combinationSum3(int k, int n) {
vector<vector<int>> ans;
vector<int> path;
int sum = 0;
std::function<void(int, int)> dfs = [&] (int i, int nums){
int d = k - path.size(); // 还需要多少个数
if(sum == n && nums == k){
ans.push_back(path);
return;
}
// 9 - i + 1 < d 表示剩余可选的数字选完也不满足 k个数要求
if(sum > n || nums == k || (9-i+1)<d) // 提前剪枝
return;
for(int j = i; j <= 9; j++){
sum += j;
path.push_back(j);
dfs(j+1, nums+1);
// 不选 数字j,恢复现场
sum -= j;
path.pop_back();
}
};
dfs(1, 0);
return ans;
}
};
|
代码思路提出的剪枝写法,参考灵神python写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
ans = []
path = []
def dfs(i: int, t: int) -> None:
d = k - len(path) # 还要选 d 个数
if t < 0 or t > (i * 2 - d + 1) * d // 2: # 剪枝
return
if d == 0:
ans.append(path.copy())
return
for j in range(i, d - 1, -1):
path.append(j)
dfs(j - 1, t - j)
path.pop()
dfs(9, n)
return ans
|
22. 括号生成
代码思路:
这个 括号生成 和 括号嵌套是一样的,左括号的右边必须有一个对应的右括号,右括号左边也有一个对应的左括号。对于字符串的每个前缀要求:左括号的个数 >= 右括号的个数,最后整个字符串,左右括号的个数 = n。
将这道题 归类为组合型回溯,可以用以下的生成树来理解:
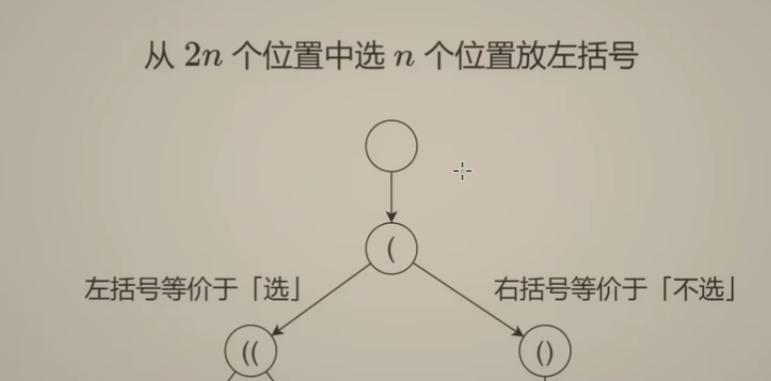
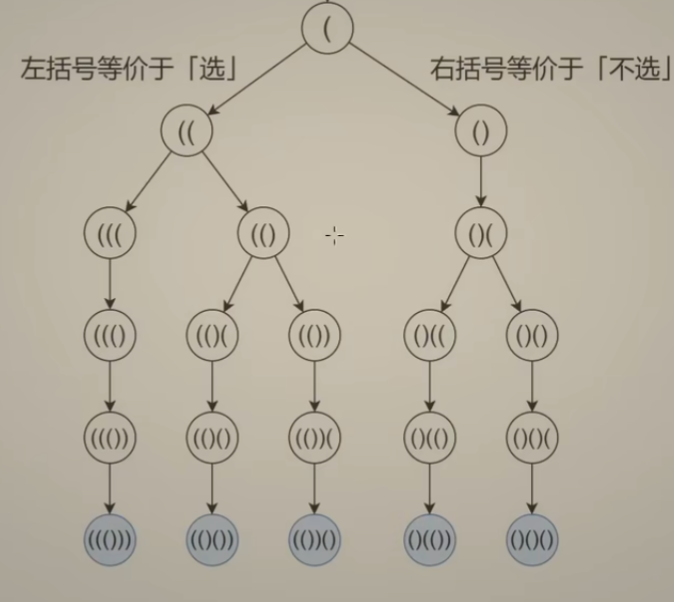
问题思考归纳如下:

两种递归分支:
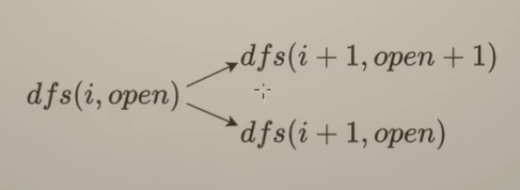
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> ans;
string path = "";
int m = n * 2;
// 下边 参数 open代表左括号 个数
// i 代表path中字符个数为 i,i从0开始 且 i < m, i == m 退出递归
// 时间复杂度:O(n * C(2n, n)),由于左右括号有限制,实际递归次数没有这么多,精确估算了解卡特兰数
// 空间复杂度:O(n)
std::function<void(int, int)> dfs = [&](int i, int open) {
if(i == m){
ans.push_back(path);
return;
}
if(open < n){
path += '(';
dfs(i+1, open+1);
path.pop_back(); // 恢复现场
}
if(i-open < open){
path += ')';
dfs(i+1, open);
path.pop_back(); // 恢复现场
}
};
dfs(0, 0);
return ans;
}
// 法二:枚举下一个左括号的位置
};
|
课后作业
换一种写法完成上面三题。
301.删除无效的括号
16 回溯 排列型 N皇后
课程大纲:

46.全排列
解题思路:
-
问题:给出一个不含 重复数字的数组,返回其所有可能的全排列。此时,全排列的个数就是 数组长度的阶乘。
-
相比组合,排列中元素的顺序是有区别的!!!,所以{1,2,3}和{1,3,2}是相同的组合,却是不同的排列。
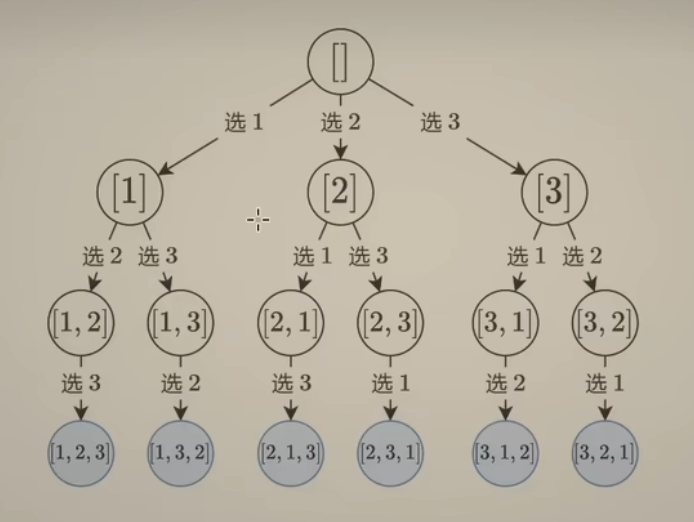
-
选了一个数之后,如何让递归下一层的函数知道还能选择哪一个数呢?
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
class Solution {
public:
// 法一:使用 flag哈希表来 存储是否选择的数(自己的做法)
vector<vector<int>> permute(vector<int>& nums) {
map<int, bool> mp;
for(int i = 0; i < nums.size(); ++i){
mp[nums[i]] = true;
}
vector<int> vals;
vector<vector<int>> ans;
std::function<void(int)> dfs = [&](int i){
mp[nums[i]] = false;
vals.push_back(nums[i]);
for(int j = 0; j < nums.size(); ++j){
// 当前数字可用
if(mp[nums[j]]){
dfs(j);
// 恢复现场
mp[nums[j]] = true;
vals.pop_back();
}
}
// 完成全排列,将排列一种情况 push到 ans中,返回
if(vals.size() == nums.size()){
ans.push_back(vals);
return;
}
};
// 如果只是 调用 dfs(0),那么只能生成 以nums[0]开头的排列组合
// 缺少其他 nums[i]开头的排列组合,此时需要 遍历整个nums数组,
// 传入数组每个元素让其能够保证每个元素都排在第一位
for(int i = 0; i < nums.size(); ++i){
// dfs(nums[i]); // 这里应该传入nums数组下标i 来保证传入的顺序,
// 如果使用nums[i]传入,函数内访问nums[nums[i]]可能会数组越界
dfs(i);
// 恢复现场
mp[nums[i]] = true;
vals.pop_back();
}
return ans;
}
// 法二:使用数组path 记录路径上的已选数字,集合s记录剩余未选数字
vector<vector<int>> permute1(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> ans;
vector<int> path(n), on_path(n);
// 参数说明:
// i 表示需要构造大于等于 i的排列,s 表示数组中剩余可以选的数
function<void(int)> dfs = [&](int i) {
if(i == n){
ans.emplace_back(path);
return;
}
for(int j = 0; j < n; ++j){
// 这里的 on_path[j] 相当于 flag作用,来检索当前下标j对应的nums[j]是否也是可用的
if(!on_path[j]){
path[i] = nums[j];
on_path[j] = true;
dfs(i+1);
on_path[j] = false; // 恢复现场
}
}
};
dfs(0);
return ans;
}
};
|
**灵神写法:**完整对应法二,使用Python写更加直观
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
ans = []
path = [0] * n
on_path = [False] * n
def dfs(i :int) -> None:
if i == n:
ans.append(path.copy())
return
for j, on in enumerate(on_path):
if not on:
path[i] = nums[j]
on_path[j] = True
dfs(i+1)
on_path[j] = False # 恢复现场
dfs(0)
return ans
|
时间复杂度:可以用:叶子个数 * 根到叶子的路径长度 来计算,这样时间复杂度为O(n * n!),当然这样是每条路径都计算了一遍,对于上层的根结点来说,由于是路径上共享的节点,会被重复统计很多次。
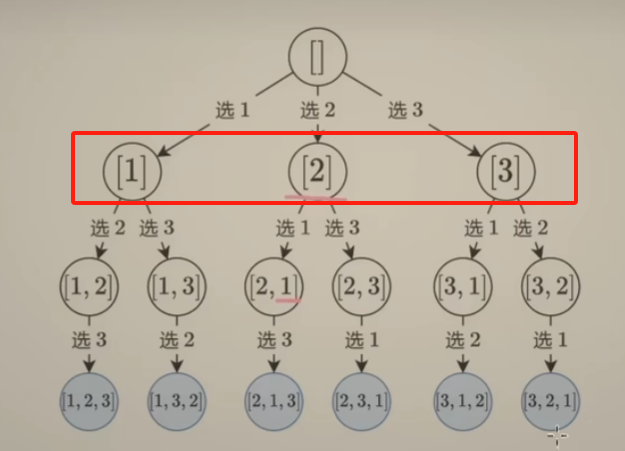
思考:有没有更加精确的办法,直接计算这棵树有多少个节点? 知道了节点个数,也就知道了递归的次数。
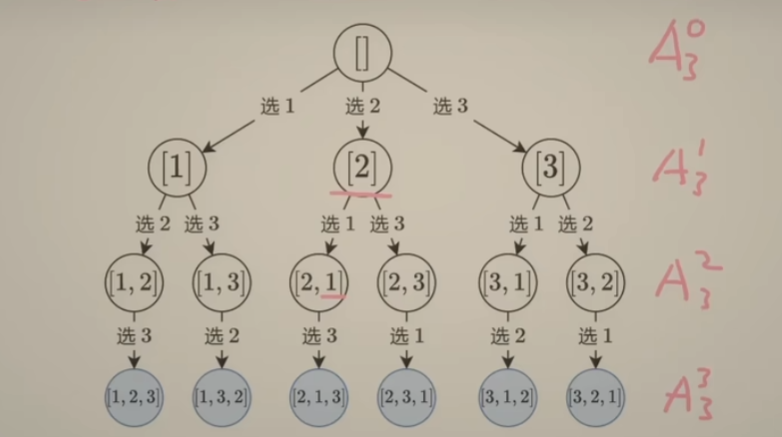
使用排列组合的方式来计算,每一层所需的元素个数为m,总的要排列元素数为n,则每一层的结点数为C(m, n)
累加一下,得到如下精确计算公式: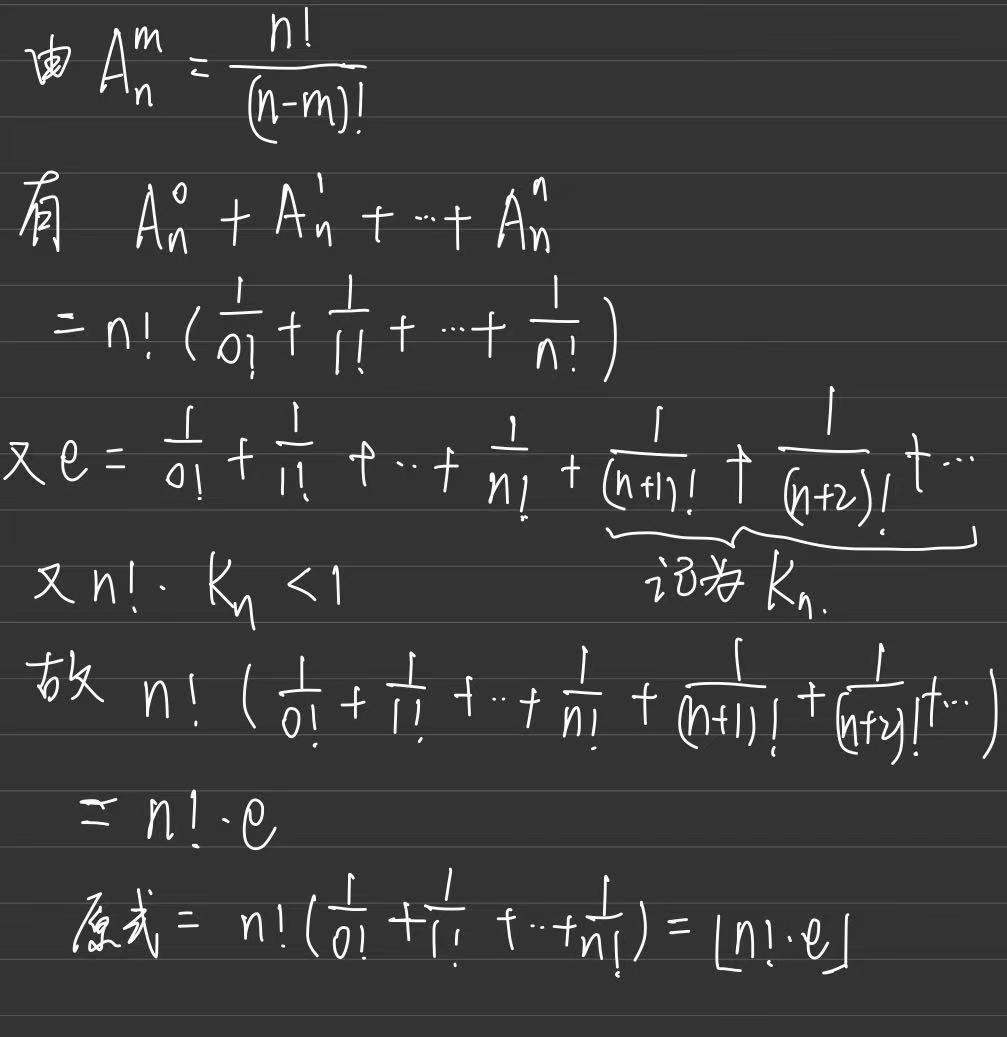
在大O标记算法复杂度中,估计算法的上界:
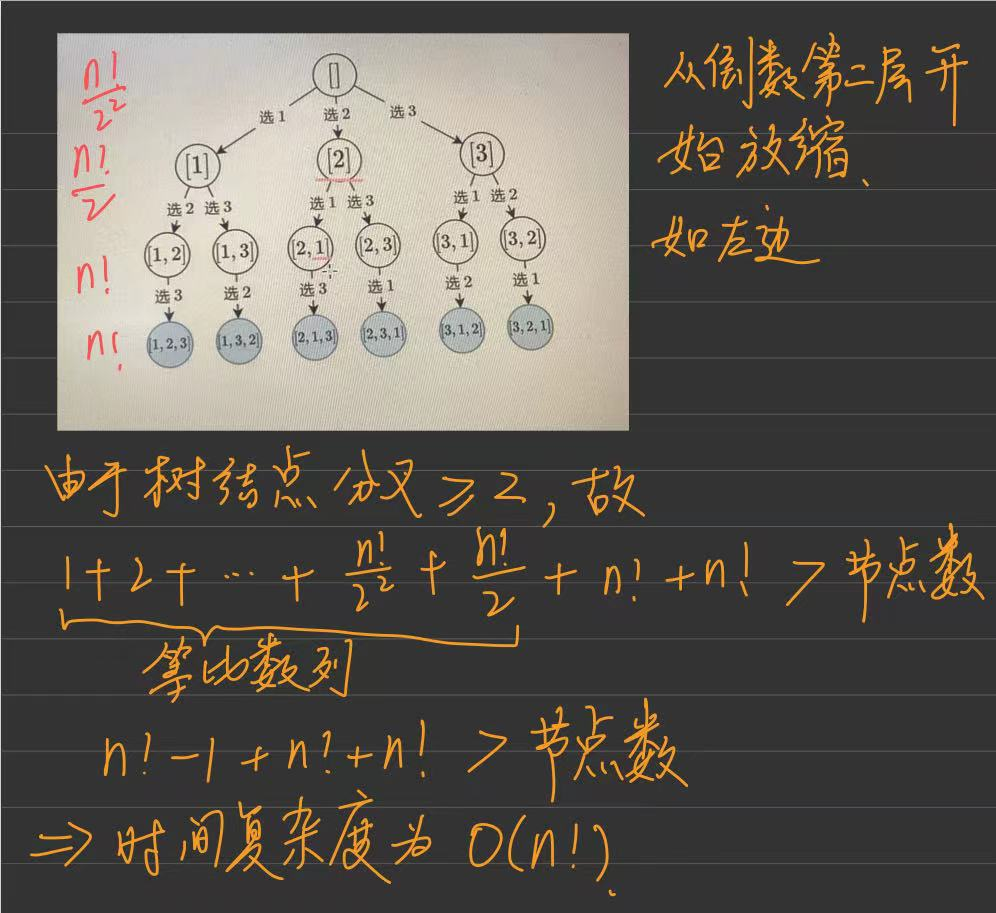
节点个数知道了 ,每个叶子结点复制新数组时间复杂度为O(n),总的时间复杂度为O(n * n!)
[灵神完整分析:时间复杂度:O(n⋅n!),其中 n为 nums的长度。搜索树中的节点个数低于 3⋅n!。实际上,精确值为 ⌊e⋅n!⌋,其中 e=2.718⋯ 为自然常数。每个非叶节点要花费 O(n)的时间遍历 onPath数组,每个叶结点也要花费 O(n)的时间复制 path数组,因此时间复杂度为 O(n⋅n!)]
空间复杂度:除去答案,其余用到的空间为O(n)
51.N 皇后
解题思路:

使用一个 col数组,记录第 i 行的皇后在第 col[i]列,col数组就是一个0~n-1 的排列。若是只有不同行和不同列不同这两个要求,那么这一题和全排列是等价的。
n皇后比 全排列多了一个限制: 不同皇后不能处于同一斜线。这需要如何表示?一次函数求截距,截距一致表示有不同皇后在 同一个斜线上
从上到下枚举的皇后位置,故这里只需要 看看左上方向 or 右上方向 有无皇后同一斜线即可:
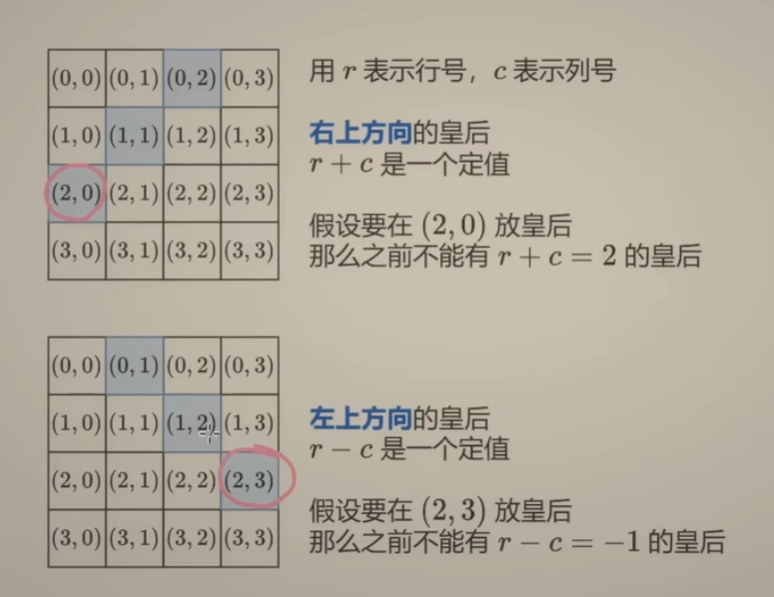
优化:

使用 哈希表 或者 布尔数组对上述的 r+c 和 r-c进行优化判断。
- 时间复杂度:O($n^2$ ⋅n!)。搜索树中至多有 O(n!)个叶子,每个叶子生成答案每次需要 O($n^2$ ) 的时间,所以时间复杂度为 O($n^2$⋅n!)。实际上搜索树中远没有这么多叶子,n=9时只有 352 种放置方案,远远小于 9!=362880。
- 空间复杂度:O(n)。返回值空间不计。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
class Solution {
private:
// r 表示行号 c 表示列号
// 这个函数使用 循环用于solveNQueens函数判断 当前位置能不能放皇后,导致其时间复杂度为O(N)
// 下边对这个进行优化,将复杂度优化为O(1)
bool isValid(int r, int c, vector<int> &col){
for(int R = 0; R < r; ++R)
if(r+c == R+col[R] || r-c == R-col[R]) return false;
return true;
}
public:
// 写法一:从上到下枚举的皇后位置,故这里只需要 看看 左上方向 or 右上方向 有无皇后同一斜线即可
// 15ms 击败 24.35% 使用 C++ 的用户
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> ans;
vector<int> col(n, 0);
set<int> col_index;
for(int i=0;i<n;i++){
col_index.insert(i);
}
// r表示 当前要枚举的行号;s表示 剩余可以枚举的列号
function<void(int, set<int>&)> dfs = [&] (int r, set<int> &s) {
// 使用O(n^2)时间复杂度生成棋盘
if(r == n){
vector<string> board(n);
for(int i = 0; i < n; ++i){
board[i] = string(col[i], '.') + 'Q' + string(n - 1 - col[i], '.');
}
ans.push_back(board);
return;
}
// r表示行号 ; c表示列号 ; col[i]表示第i行col[i]列放着一个皇后
for(auto c : s){
if(isValid(r, c, col)){
col[r] = c;
set<int> s2 = s;
s2.erase(c);
dfs(r+1, s2);
}
}
};
dfs(0, col_index);
return ans;
}
// 写法二:优化 判断位置是否可以放置皇后 从上边isValid函数O(n)复杂度 ——> 当前使用三个布尔数组O(1)复杂度
// 4ms 击败92.00% 使用 C++ 的用户
vector<vector<string>> solveNQueens1(int n){
vector<vector<string>> ans;
// col数组:表示 第i行 存放皇后位置在 col[i]列处
// on_path数组:表示第c列中 是否有皇后,有on_path[c] = true
vector<int> col(n), on_path(n);
// 数组下标 用于表示 不同斜线截距,相同截距若是有放置皇后,则置为 true
vector<int> diag1(n*2-1), diag2(n*2-1);
// r表示 当前要枚举的行号
function<void(int)> dfs = [&](int r) {
if(r == n) { // 构造对应的棋盘答案
vector<string> board(n);
for(int i = 0; i < n; ++i)
// 由于 col[i]中保存的Q位置是 数组下标开始的 也就是从0开始的下标,而实际Q位置应该从1开始
// 所以下边利用这个性质 来构造每一行皇后的位置
board[i] = string(col[i], '.') + 'Q' + string(n-1-col[i], '.');
ans.emplace_back(board);
return;
}
for(int c = 0; c < n; ++c){
int rc = r-c+(n-1);
if(!on_path[c] /* 当前列c没有皇后 */ && !diag1[r+c] && !diag2[rc]){
col[r] = c; // 当前行 r的皇后在 c列
on_path[c] = diag1[r+c] = diag2[rc] = true;
dfs(r+1); // 递归第 r+1 行
on_path[c] = diag1[r+c] = diag2[rc] = false; // 恢复现场
}
}
};
dfs(0);
return ans;
}
};
|
课后作业
52.N 皇后 II
提示:和51题一样,只不过这个题目不用构造答案,而是返回 解法个数。
- 时间复杂度:由于不用构造答案,不用额外花费O($n^2$) 时间复杂度,总的时间复杂度为:O(n · n!),当然是指优化后判断是否能放皇后O(1)处理的情况
- 空间复杂度:O(n)。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
// 0ms 100.00% 使用 C++ 的用户
int totalNQueens(int n) {
int count = 0; // 解法个数
// col数组:表示 第i行 存放皇后位置在 col[i]列处
// on_path数组:表示第c列中 是否有皇后,有on_path[c] = true
vector<int> col(n), on_path(n);
// 数组下标 用于表示 不同斜线截距,相同截距若是有放置皇后,则置为 true
vector<int> diag1(n*2-1), diag2(n*2-1);
// r表示 当前要枚举的行号
function<void(int)> dfs = [&](int r) {
if(r == n) { // 构造对应的棋盘答案
count++; // 解法+1
return;
}
for(int c = 0; c < n; ++c){
int rc = r-c+(n-1);
if(!on_path[c] /* 当前列c没有皇后 */ && !diag1[r+c] && !diag2[rc]){
col[r] = c; // 当前行 r的皇后在 c列
on_path[c] = diag1[r+c] = diag2[rc] = true;
dfs(r+1); // 递归第 r+1 行
on_path[c] = diag1[r+c] = diag2[rc] = false; // 恢复现场
}
}
};
dfs(0);
return count;
}
};
|
17 动态规划 从记忆搜索到递推 打家劫舍
DP讲解:
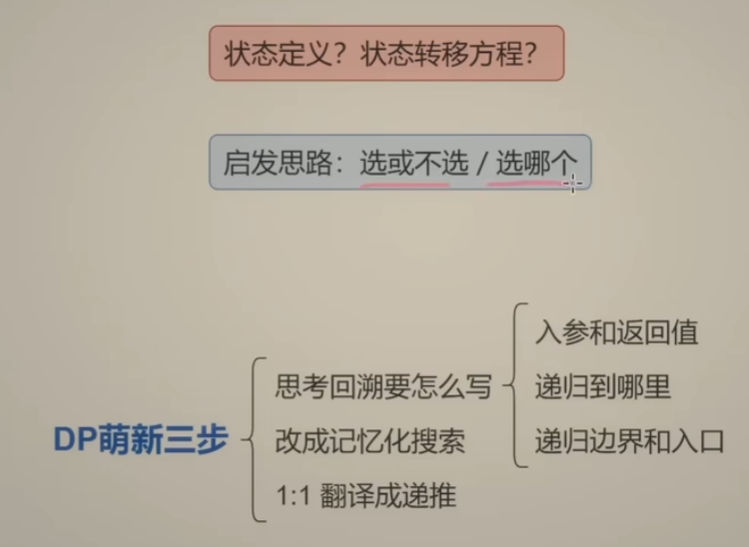
回溯—> 记忆化搜索(带备忘录的回溯)—>动态规划
198.打家劫舍
解题思路:
-
回溯思考:相邻房间不能选,从最后一个房间(编号为n)考虑问题
- 若最后一个房间选,则 只能从编号为[1, n-2]的房间进行选择
- 若最后一个房间不选,则 可以从编号为[1, n-1]的房间进行选择
画出搜索树状图,如下:
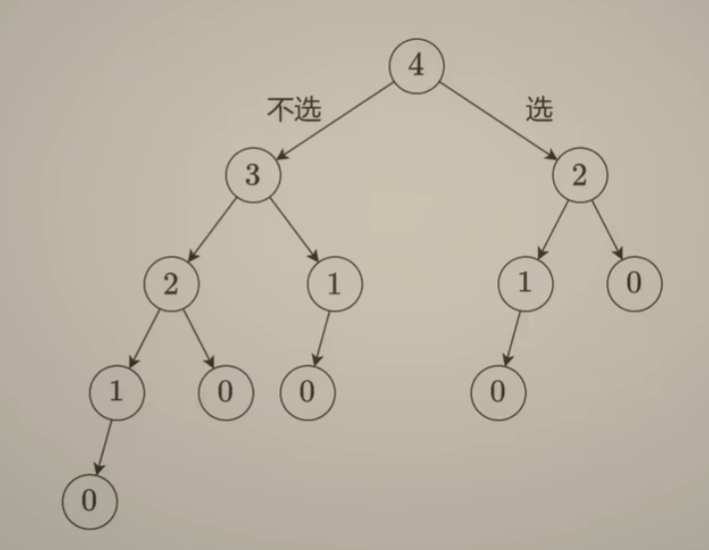
将上面的分类,归结为 “回溯三问”,如下:

回溯的时间复杂度为 指数级别的。
-
观察到上边搜索树中,有一部分 树的结点是重复计算的,可以第一次计算的时候就保存到一个全局数组中,之后就不用重复计算了,这种思想也称为"记忆化搜索”
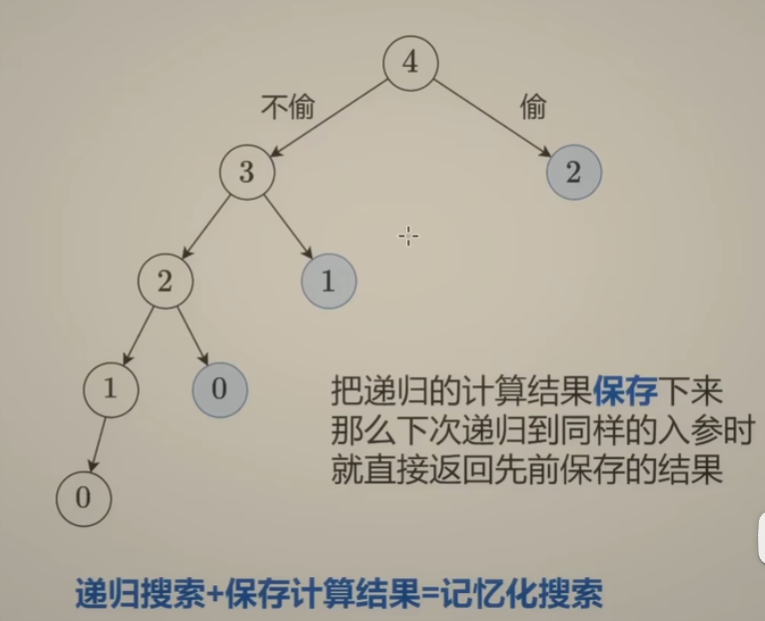
优化后的搜索树只有 O(n)个结点,因此时间复杂度也优化到O(n)
-
从记忆化搜索 —> 递推(动态规划)

时间复杂度为:O(n),空间复杂度 仍然为O(n)
-
优化动态规划的时间复杂度,采用 滚动数组的技巧,长度取决于递推关系式前后依赖的数值数量

- 时间复杂度:O(n)
- 空间复杂度:O(1). 仅用到若干额外变量
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
// 动态规划的的四个解题步骤是:
//1. 定义子问题
//2. 写出子问题的递推关系
//3. 确定 DP 数组的计算顺序
//4. 空间优化(可选)
class Solution {
public:
// 动态规划
int rob(vector<int>& nums) {
// 原问题:
// f(n):从[1, n] 房间中偷取的最大金额
// 子问题:
// f(k): 从[1, k] 房间中偷取的最大金额
// 初始条件:f(0) = 0, f(1) = nums[0] // 数组从下标0开始,而房间数量从1开始
// 递归式子:f(k) = max(f(k-1), f(k-2) + nums[k-1])
// - f(k-1)表示 第k间房间不偷,前k-1间房间偷
// - f(k-2)表示 第k间房间 和 前k-2间房间 偷,第k-1间房间不偷
int n = nums.size();
vector<int> dp(n+1, 0);
dp[1] = nums[0];
for(int k = 2; k <= n; ++k){
dp[k] = max(dp[k-1], dp[k-2]+nums[k-1]);
}
return dp[nums.size()];
}
// 法一:回溯做法
// 回溯时间复杂度为指数级别 递增,会超时
int rob1(vector<int> &nums) {
int n = nums.size();
function<int(int)> dfs = [&](int i) {
if(i < 0)
return 0;
int res = max(dfs(i - 1), dfs(i - 2) + nums[i]);
return res;
};
return dfs(n-1);
}
// 法二:记忆化搜索
// 将重复计算的结果保存到 一个数组中 每次要计算之前先查看数组是否有计算好的结果
int rob2(vector<int> &nums) {
int n = nums.size();
vector<int> memo(n, -1); // 初始化memo数组 大小为n 值为-1
function<int(int)> dfs = [&](int i) {
if(i < 0)
return 0;
if(memo[i] != -1)
return memo[i];
int res = max(dfs(i - 1), dfs(i - 2) + nums[i]);
memo[i] = res;
return res;
};
return dfs(n-1);
}
// 法三:从记忆化搜索 到 递推
// 空间复杂度 仍为 O(n)
int rob3(vector<int> &nums) {
int n = nums.size();
vector<int> f(n + 2);
for (int i = 0; i < n; ++i)
f[i + 2] = max(f[i + 1], f[i] + nums[i]);
return f[n + 1];
}
// 法四:动态规划
// 空间优化为 O(1)
int rob4(vector<int> &nums) {
int f0 = 0, f1 = 0;
for (int x : nums) {
int new_f = max(f1, f0 + x);
f0 = f1;
f1 = new_f;
}
return f1;
}
};
|
课后作业
70.爬楼梯
746.使用最小花费爬楼梯
2466.统计构造好字符串的方案数
213.打家劫舍 II
18 0-1背包 完全背包 目标和 零钱兑换
学习大纲:
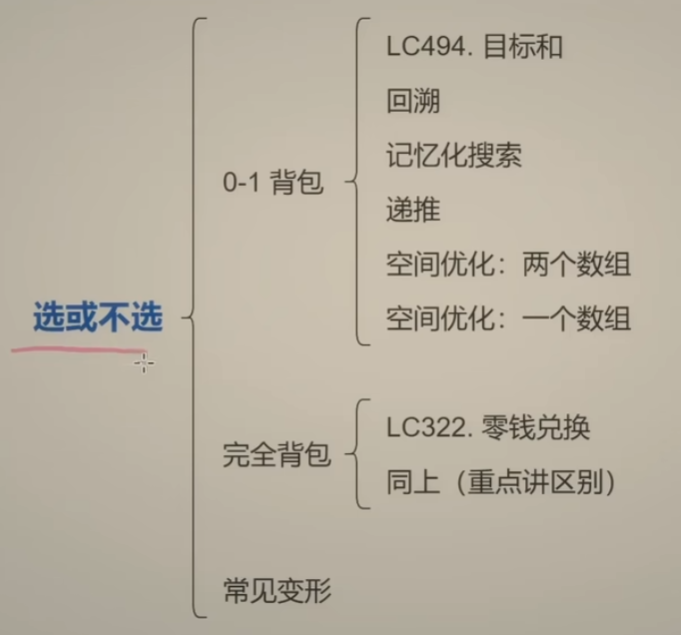
解题思路:
1、0-1背包:有n个物品,第 i 个物品的体积为 w[i],价值为 v[i]。每个物品至多选一个,求体积和 不超过 capacity 时的最大价值和

0-1背包参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# capacity:背包容量
# w[i]: 第i个物品的体积
# v[i]: 第i个物品的价值
# 返回值:所选物品体积和不超过 capacity 的前提下,所能得到的最大价值和
def zero_one_knapsack(capacity: int, w: List[int], v: List[int]) -> int:
n = len(w)
@cache # 改成记忆化搜索,python可以添加一个cache装饰器,而其他语言可以用 一个cache数组存储
def dfs(i, c):
if i < 0:
return 0
if c < w[i]:
return dfs(i-1, c) # 背包剩余容量c 不够装下w[i]
return max(dfs(i-1, c), dfs(i-1, c-w[i]) + v[i])
return dfs(n-1, capacity) # 从背包最后一个 物品开始枚举,其实剩余容量为capacity
|
推荐学习路线:二叉树递归—> 回溯—> 记忆化搜索—> 递推
-
目标和 494.目标和
将原问题转化如下:

选一些数 ,这些数的和恰好等于一个特定数(sum)的方案数 — 0-1背包的常见变形
把上边0-1背包,最大和计算公式:
1
|
dfs(i, c) = max(dfs(i-1, c), dfs(i-1, c-w[i]) + v[i]);
|
改为:
1
|
dfs(i, c) = dfs(i - 1, c) + dfs(i - 1, c - w[i]);
|
这里函数参数解释:
dfs(i, c):表示从前 i 个数中选取一些数 恰好组成c的方案数- 这里使用加法原理:方案数 是小一级子问题的总和
法一:递归+数组保存= 记忆化搜索
- 时间复杂度:O(n⋅(target+S)),其中 n为
nums的长度,S为 nums 的元素之和。
- 空间复杂度:O(n⋅(target+S))
法二:递归—> 循环递推
- 时间复杂度:O(n⋅(target+S)),其中 n为
nums 的长度,S 为 nums 的元素之和
- 空间复杂度:O(n⋅(target+S))
法三:空间优化:滚动数组

从上面的递推式子,可以看出,每次计算出$f[i][c]$ 或者 $f[i][c-w[i]]$ 之后,$f[i+1][c]$ 只依赖这两个元素,而不关$f[i-1][c] 和 f[i-1][c-w[i]]$ 什么事了,可以用列为2的二维数组,也就是两个一维数组来存储计算中间值即可。
- 时间复杂度:O(n⋅(target+S)),其中 n为
nums 的长度,S 为 nums 的元素之和
- 空间复杂度:O((target+S))
法四:空间优化,使用一个数组来存储动态规划的中间状态(==非常难想,还没怎么理解,之后再来看看==)

将 $f[i+1][c]和f[i][c]$合并到同一个数组中,从左向右计算,会把结果给覆盖掉,导致计算出错。改为:从右往左算,即从数组后边算到前边
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
|
class Solution {
public:
// 法一:递归
int findTargetSumWays(vector<int>& nums, int target) {
// 添加正数的和 为p
// 添加负数的绝对值 为s - p(s为所有元素的和)
// target = p - (s-p) = 2p - s
// p = (s+t) / 2
// 原问题转化为:从 nums中选择一些数字,使得其和 为(s+t)/2
// 由于nums[i]>=0,所以(s+t) 也是非负数
for(int i = 0; i < nums.size(); ++i)
target += nums[i];
if(target < 0 || target % 2)
return 0; // target(s+t 之后的数)不能为 奇数,因为p = (s+t)/2,为整数
target /= 2;
int n = nums.size();
function<int(int, int)> dfs = [&](int i, int c){
// 修改边界条件
// 下边为原来的边界条件
// if(i < 0)
// return 0;
if(i < 0)
return c == 0 ? 1 : 0; // c=0,表示找到一个合法方案;c!=0,合法方案为0
if(c < nums[i])
return dfs(i - 1, c);
return dfs(i - 1, c) + dfs(i - 1, c - nums[i]);
};
return dfs(nums.size()-1, target);
}
// 法二:记忆化搜索 没通过测试...
int findTargetSumWays1(vector<int>& nums, int target){
for(int i = 0; i < nums.size(); ++i)
target += nums[i];
if(target < 0 || target % 2)
return 0; // target(s+t 之后的数)不能为 奇数,因为p = (s+t)/2,为整数
target /= 2;
int n = nums.size(), cache[n][target+1];
memset(cache, -1, sizeof(cache)); // -1表示没有访问过
function<int(int, int)> dfs = [&](int i, int c){
// 修改边界条件
// 下边为原来的边界条件
// if(i < 0)
// return 0;
if(i < 0)
return c == 0 ? 1 : 0; // c=0,表示找到一个合法方案;c!=0,合法方案为0]
int& res = cache[i][c];
if(res != -1) return res;
if(c < nums[i])
return res = dfs(i - 1, c); // res引用,传递最新结果更新数组,并且作为返回值
return dfs(i - 1, c) + dfs(i - 1, c - nums[i]);
};
return dfs(nums.size()-1, target);
}
// 法三:动态规划,二维数组递推
int findTargetSumWays2(vector<int>& nums, int target){
for(int i = 0; i < nums.size(); ++i)
target += nums[i];
if(target < 0 || target % 2)
return 0; // target(s+t 之后的数)不能为 奇数,因为p = (s+t)/2,为整数
target /= 2;
int n = nums.size(), f[n+1][target + 1];
memset(f, 0, sizeof(f));
f[0][0] = 1;// 第一行第一个数为1,其余数为0 因为 数组第0个元素不存在,此时 c!=0,背包容量还剩余 不符合条件
// 第一列 第一行为1, 其余行虽然 c=0 背包容量归零了,但是还有枚举 剩余数字权力,后边 更新实际的方案数
for(int i = 0; i < n; ++i)
for(int c = 0; c <= target; ++c){
if(c < nums[i]) f[i+1][c] = f[i][c];
else f[i+1][c] = f[i][c] + f[i][c-nums[i]];
}
return f[n][target];
}
// 法四:空间优化,滚动数组
int findTargetSumWays3(vector<int>& nums, int target){
for(int i = 0; i < nums.size(); ++i)
target += nums[i];
if(target < 0 || target % 2)
return 0;
target /= 2;
int n = nums.size();
int f[2][target+1];
memset(f, 0, sizeof(f));
f[0][0] = 1;
for(int i = 0; i < n; ++i)
for(int c = 0; c <= target; ++c){
if(c < nums[i]) f[(i+1)%2][c] = f[i%2][c];
else f[(i+1)%2][c] = f[i%2][c] + f[i%2][c-nums[i]];
}
return f[n%2][target]; // 所有数组 第一维度都 改为 %2,这样就可以在第一二列来回切换计算值
}
// 法五:空间优化为 一维数组
int findTargetSumWays4(vector<int>& nums, int target){
for(int i = 0; i < nums.size(); ++i)
target += nums[i];
if(target < 0 || target % 2)
return 0;
target /= 2;
int n = nums.size();
int f[target+1];
memset(f, 0, sizeof(f));
f[0] = 1;
// 初始版本
for(int i = 0; i < n; ++i)
for(int c = target; c >= 0; c--){
if(c < nums[i]) // 由于 f[c] = f[c] 没有任何意义,所以只需要讨论c>=nums[i]情况
f[c] = f[c]; // f[i+1][c] = f[i][c]
else
f[c] = f[c] + f[c-nums[i]];
}
// 简化版本
// for(int i = 0; i < n; ++i){
// for(int c = target; c >= nums[i]; --c)
// f[c] += f[c-nums[i]];
// }
return f[target];
}
};
|
3、完全背包:有n个物品,第i种物品的体积为 w[i],价值为v[i]。每种物品无限次重复选,求体积和 不超过capacity时的 最大价值和

完全背包与上边0-1背包的唯一区别:一个物品可以选择多次,或者不选
- 完全背包状态转移:
dp[i][c] = max(dp[i-1][c], dp[i][c - w[i]] + v[i])
- 可以看到上边
dp[i][c-w[i]] 表示选择当前物品i,还可以重复选择
- 0-1背包状态转移:
dp[i][c] = max(dp[i-1][c], dp[i][c - w[i]] + v[i])
- 可以看到上边
dp[i-1][c-w[i]] 表示选择当前物品i,不可以再选择了
-
零钱兑换 322.零钱兑换
将原问题 转化为如下问题:把上边状态转移等式,物品价值v[i]看作1,表示物品个数;把求最大总价值(最大物品个数) 改为 求最小总价值(最小物品个数)

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
// 法一:记忆化搜索
int coinChange(vector<int>& coins, int amount) {
int n = coins.size(), cache[n][amount+1];
memset(cache, -1, sizeof(cache)); // -1 表示没有访问过
function<int(int, int)> dfs = [&](int i, int c) -> int {
if(i < 0) return c==0 ? 0 : INT32_MAX / 2; //除 2 是防止下面 + 1 溢出
int &res = cache[i][c]; // 引用 res改变,cache[i][c]也会改变
if(res != -1) return res;
if(c < coins[i]) return res = dfs(i-1,c);
return res = min(dfs(i-1, c), dfs(i, c-coins[i]) + 1);
};
int ans = dfs(n-1, amount);
// 这里 return ans < INT32_MAX ? ans : -1;
// 会有样例过不了:coins = [2] amount = 3
// 输出:1073741823(估计 就是INT32_MAX/2) 预期结果:-1
return ans < INT32_MAX/2 ? ans : -1;
}
// 法二:将记忆化搜索 翻译成 递推
// 需要注意两点:初始化 f[0][0] = 0,其余f元素初始化为无穷大,因为这道题要求最小硬币数
// min取最小值,可以每次将无穷大的选法 排除
int coinChange1(vector<int>& coins, int amount){
}
// 视频看到 13.10
};
|
课后作业
2915.和为目标值的最长子序列的长度
416.分割等和子集
279.完全平方数
518.零钱兑换 II
19 线性DP 最长公共子序列LCS 编辑距离
学习大纲:

默认情况下,子数组和子串 是连续的;子序列不一定是连续的,例如:abcde中,ace就是一个子序列。
子序列定义:由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串
最长公共子序列:所有公共子序列中,取最大值。
1143.最长公共子序列
解题思路:
类比子序列,考虑每个字符串中的字母 选 或者 不选,从最后一个字母开始考虑,两两组合就有四种情况

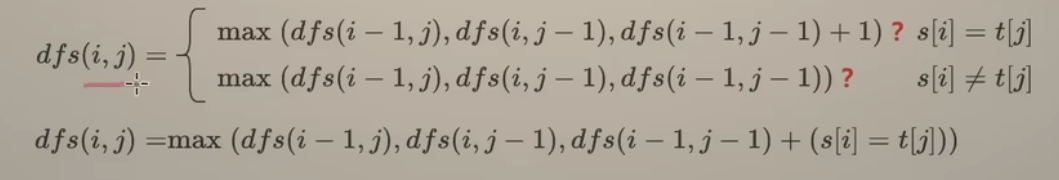
思考如下问题:

从上边反证法,可以得到结论:
- $s[i] = s[j]$ 时,不需要考虑 $dfs(i - 1, j)$ 和 $dfs(i, j - 1)$的情况(这两个情况获得的最长公共子序列 不会大于 $dfs(i-1, j-1)$即选择了$s[i]与s[j]$时的最大公共子序列)
- $s[i] \ne s[j]$ 时,由于$dfs(i-1, j)$ 和 $dfs(i, j-1)$中最终会递归到$dfs(i-1, j-1)$的情况,所以不需要考虑$dfs(i - 1, j- 1)$
最终简化后的递推式子,如下:
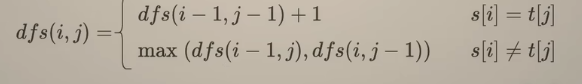

优化:
从上边的递推式子可以看出,如果把状态填入二维表格,那么当前计算的状态 只和 左边一个状态、上边一个状态、还有左上角一个状态有关,可以按照优先行填充方法 从左往右、从上到下填充二位数组,即可求出:$f[n][m]$
**使用一个数组计算最终状态:**从上边的填表顺序可以看出,使用两个一维数组就可以完成整个过程迭代。不过现在想用一个一维数组达到同样的效果,那么在计算 $f[i][j]$ 的时候,在一维数组中就是 $f[j]$ 依赖于 前边刚计算的$f[j-1]$,还有上一轮计算的 $f[j]$,剩下上一轮计算的 $f[j-1]$被这一轮计算的 $f[j-1]$覆盖掉了。那么需要使用一个临时变量将上一次计算的$f[j-1]$保存下来,再计算这一轮的$f[j-1]$。如此迭代 n次,就可以得到最终结果:$f[m]$
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
class Solution {
public:
// 法一:记忆化搜索
int longestCommonSubsequence(string text1, string text2) {
int n = text1.length(), m = text2.length();
int cache[n][m];
// Code analysis has been suspended
memset(cache, -1, sizeof(cache)); // 初始化为-1,表示没有访问过
function<int(int, int)> dfs = [&](int i, int j) -> int {
if(i < 0 || j < 0) return 0;
int &res = cache[i][j]; // 引用,res修改,cache也会跟着修改
if(res != -1) return res;
if(text1[i] == text2[j]) {
return res = dfs(i - 1, j - 1) + 1;
} else {
return res = max(dfs(i - 1, j), dfs(i, j - 1));
}
};
return dfs(n-1, m-1); // 由于要访问数组下标,所以这里的参数都应该-1
}
// 法二:改成递推
// 一比一翻译,注意:为了避免出现负数下标,需要将上述的 i-1 改为 i,j-1也改为 j
int longestCommonSubsequence1(string text1, string text2) {
int n = text1.length(), m = text2.length();
int f[n+1][m+1];
memset(f, 0, sizeof(f));
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j){
if(text1[i] == text2[j]){
f[i+1][j+1] = f[i][j] + 1;
} else {
f[i+1][j+1] = max(f[i][j+1], f[i+1][j]);
}
// 也可以改写成 三目运算符
// f[i+1][j+1] = (tex1[i] == text2[j]) ? f[i][j]+1 : max(f[i][j+1], f[i+1][j]);
}
// return f[n+1][m+1]; 返回错下标 越界了
return f[n][m];
}
// 法三:空间优化,使用滚动数组
int longestCommonSubsequence2(string text1, string text2){
int n = text1.length(), m = text2.length();
int f[2][m+1];
memset(f, 0, sizeof(f));
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j) {
// 下边的 text1 == text2 直接对比两个字符串了 难怪没通过测试样例
// f[(i+1)%2][j+1] = text1 == text2 ? f[i%2][j]+1 : max(f[i%2][j+1], f[(i+1)%2][j]);
f[(i+1)%2][j+1] = text1[i] == text2[j] ? f[i%2][j]+1 : max(f[i%2][j+1], f[(i+1)%2][j]);
}
return f[n%2][m];
}
// 法四:空间优化,一个一维数组,另外一维作为 迭代次数,迭代n次就可以得到结果
// 这个有个测试样例 没有通过
// "mhunuzqrkzsnidwbun"
// "szulspmhwpazoxijwbq"
// 输出:8 预期结果:6
int longestCommonSubsequence3(string text1, string text2){
int n = text1.length(), m = text2.length();
int f[m+1];
memset(f, 0, sizeof(f));
int pre = f[0]; // 保留上一轮的 前一个状态
int tmp;
for(int i = 0; i < n+1; ++i) // 迭代轮数,总共需要迭代n+1次,才可以达到和二维数组 第n行的结果
for(int j = 0; j < m; ++j) {
tmp = f[j+1]; // 保留上一轮的 前一个状态
f[j+1] = text1[i] == text2[j] ? pre+1 : max(f[j+1], f[j]); // 更新这一轮的当前状态
pre = tmp;
}
return f[m];
}
};
|
时间复杂度:O(n $\times$ m),可以用上边计算公式:状态个数 $\times$ 单个状态计算时间
空间复杂度(没优化的前):O(n $\times$ m)
72.编辑距离
解题思路:
类比上一题,最长公共子序列中,原问题和子问题的递归式子,等价转换如下:

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
// 法一:动态规划 + 滚动数组优化
int minDistance(string word1, string word2) {
// 题意:经过最少操作数,将 word1 转换为 word2
// 可以对 word1 进行三种操作:插入、删除、替换一个字符
int n = word1.length(), m = word2.length();
int f[2][m+1];
// 初始化数组
//1. 当 n = 0的时候,需要进行 m次插入操作 转换为 word2
// 注意下边循环 终止条件应该为: j <= m 要初始化所有情况
// 不然样例:word1 = "" word2 = "" 过不了,究其原因是:最后返回f[0][m] 但是没初始化
for(int j = 0; j <= m; ++j) f[0][j] = j;
// memset(f, 0, sizeof(f)); // 初始化有问题
for(int i = 0; i < n; ++i){
// 2. 当 m = 0的时候,需要进行 n次删除操作,转换为 word2
f[(i+1)%2][0] = i+1; // 下标为 i+1, 同理也需要进行i+1 次操作
for(int j = 0; j < m; ++j){
if(word1[i] == word2[j]) f[(i+1)%2][j+1] = f[i%2][j]; // 不用操作
// 所有的代码都没有问题,就是下边这个分支 忘记添加一个else 导致样例过不了 找了快一个小时了...
else f[(i+1)%2][j+1] = min(f[(i+1)%2][j], min(f[i%2][j+1], f[i%2][j])) + 1; // 从左到右,分别是:插入、删除、替换操作
}
}
return f[n%2][m];
}
};
|
和上一次一样,这个代码可以使用普通二维数组(一对一翻译 记忆化搜索),也可以使用一个一维数组进行优化。
课后作业
583.两个字符串的删除操作
712.两个字符串的最小ASCII删除和
1458.两个子序列的最大点积
97.交错字符串
20 线性DP 最长递增子序列 LIS
学习大纲:
递增子序列(IS, Increasing Subsequence)—> 最长递增子序列(LIS, Longest Increasing Subsequence)
- 方案一:回溯→记忆化搜索→递推,O($n^2$)时间复杂度
- 方案二:二分+贪心,O($nlogn$) 时间复杂度
300. 最长递增子序列
解题思路:
子序列本质上 是数组的子集,可以用子集型回溯来思考。
-
思路1: 选 或 不选。为了比大小,==需要知道上一个选的数字==,比较麻烦
-
思路2: 枚举选哪个。比较当前选的数字 和 ==下一个要选的数字==
- 直接枚举 前面比 当前数小的数字即可(==枚举顺序是 从右往左枚举==)
- 只需要 一个参数,就是当前已经选中最后一个数字 数组下标
 回溯
回溯
-
思路3:nums的LIS等价于 nums与排序去重后的 nums的LCS(最长公共子序列)

-
思路4:交换状态 与 状态值 — 贪心
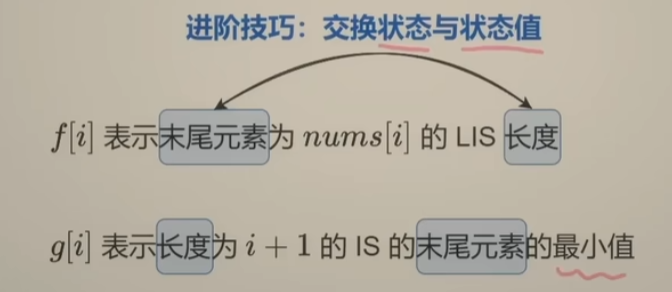

从上述更新g数组过程发现,只有定义g[i]为长度为i+1末尾元素最小值的时候,才更有机会去拓展g数组的长度。如果没有2, 4更新,末尾元素为5无法组成长度为4的上升子序列的。
注:按照上述定义的问题,没有重叠的子问题,不能算是动态规划,变成一个贪心问题。
从上边推导看出,g数组是一个严格递增的序列,每次要么修改一个数、要么添加一个数,下边进行严格证明:



上述的构造g数组的算法,使用贪心思路 + 二分查找更新数组的方式,可以达到时间复杂度为O($nlogn$),空间复杂度为O(n)。若是直接将nums数组当作g数组,只需要维护一个额外g_len变量标记当前g数组的长度,使得空间复杂度为O(1)
-
变形:如果 LIS最长递增子序列中,可以有相同元素?代码要如何修改,修改过程如何?

C++中,二分查找内置函数使用upper_bound
回溯三问:

- 递归公式:$dfs(i) = max${$dfs(j)$} + 1, $j < i 且 nums[j] < nums[i]$
- 递推公式:$f[i] = max${$f[j]$} + 1,$j < i 且 nums[j] < nums[i]$
时间复杂度:O(n)个状态,每个状态计算需要O(n)时间,总的时间复杂度为O($n^2$)
空间复杂度:O(n)
完整代码:
方案一:回溯→记忆化搜索→递推,O($n^2$)时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
class Solution {
public:
// 递归搜索
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
std::function<int(int)> dfs = [&](int i) {
int res = 0;
for(int j = 0; j < i; ++j){
if(nums[j] < nums[i]) {
res = max(res, dfs(j));
}
}
return res + 1;
};
int ans = 0;
for(int i = 0; i < n; ++i)
ans = max(ans, dfs(i));
return ans;
}
// 法二:重复子问题,优化为 记忆化搜索
int lengthOfLIS1(vector<int>& nums) {
int n = nums.size();
int memo[n];
memset(memo, 0, sizeof(memo));
std::function<int(int)> dfs = [&](int i) {
int& res = memo[i];
if(memo[i]){
return memo[i];
}
for(int j = 0; j < i; ++j){
if(nums[j] < nums[i]){
res = max(res, dfs(j));
}
}
return ++res;
};
int ans = 0;
for(int i = 0; i < n; ++i)
ans = max(ans, dfs(i));
return ans;
}
// 法三:递推写法,初始状态很重要
int lengthOfLIS2(vector<int>& nums) {
int n = nums.size();
int f[n];
// 每一个数字 都可以作为递增子序列,所以最小的递增子序列为1,
// 不过由于后边的计算每个状态逻辑首先都是不计算自己 后边得到结果才把1添加上去,所以这里也可以初始化为0
// for(int i = 0; i < n; ++i)
// f[n] = 1;
memset(f, 0, sizeof(f));
// 外层循环 计算 每个以nums[i]结尾的序列 的最长递增子序列长度
for(int i = 0; i < n; ++i){
// 内层循环 每个状态 计算的逻辑
for(int j = 0; j < i; ++j){
if(nums[j] < nums[i]){
f[i] = max(f[i], f[j]);
}
}
f[i]++; // 将 nums[i] 也添加进递增子序列里边
// 状态f[i] 真正表示 以nums[i]结尾的元素序列中 包括nums[i]最长递增子序列长度
}
// 由于 是考虑最长递增子序列,这个是有规定元素大小的 所以答案最大值 不是包括结尾元素的最长递增子序列
// 而是 整个数组中 不规定结尾元素的最长递增子序列,所以还需要遍历所有的状态值 去max
int ans = 0;
for(int i = 0; i < n; ++i)
ans = max(ans, f[i]);
return ans;
}
};
|
方案二:二分+贪心,O($nlogn$) 时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
class Solution {
public:
// 法四:贪心 + 二分查找
// 写法一:使用额外的空间
int lengthOfLIS3(vector<int>& nums){
// 1. 使用内置 lower_bound 二分查找
vector<int> g;
// 左闭右开 写二分
for(int x : nums){
auto it = lower_bound(g.begin(), g.end(), x);
if(it == g.end()) g.push_back(x); // >= x的g[j]不存在
else *it = x;
}
return g.size();
// 2. 自己手写二分
// vector<int> res;
// int len=nums.size();
// res.push_back(nums[0]);
// for (int i=1;i<len;i++) {
// if (nums[i]>res.back()) {
// res.push_back(nums[i]);
// } else {
// int l=0;
// int r=res.size()-1;
// while (l<r) {
// int m=(l+r)/2;
// if (res[m]<nums[i]) l=m+1;
// else r=m;
// }
// res[l]=min(res[l],nums[i]);
// }
// }
// return res.size();
}
// 写法二:原地修改
int lengthOfLIS4(vector<int>& nums){
auto end = nums.begin();
for(int x : nums){
// 左闭右开 [begin, end)
auto it = lower_bound(nums.begin(), end, x);
*it = x;
if(it == end) // >=x 的 g[j]不存在
++end;
}
return end-nums.begin();
}
};
|
课后作业
673.最长递增子序列的个数
1964.找出到每个位置为止最长的有效障碍赛跑路线
1671.得到山形数组的最少删除次数
354.俄罗斯套娃信封问题
1626.无矛盾的最佳球队
21 状态机DP 买卖股票系列
学习大纲:

122. 买卖股票的最佳时机 II
解题思路:
$prices = [7, 1, 5, 3, 6, 4]$
最后一天发生了什么?
**关键词:**天数、是否持有股票
子问题是什么? 到第 i 天结束时,持有/未持有股票的最大利润
下一个子问题? 到第 i-1 天结束时,持有/未持有股票的最大利润
思考另外一个问题: 在第 i 天可以进行哪些操作?
- 假设 当前第
i-1天结束时,未持有股票,那么第i天只能进行 买入操作(和不操作),会从第i-1天结束时==未持有股票状态== 跳转为 第i天结束时 ==持有股票状态==
- 假设 当前第
i-1天结束时,持有股票,那么第i天只能进行 卖出操作(和不操作),会从第i-1天结束时==持有股票状态== 跳转为 第i天结束时 ==未持有股票状态==

从上述图中可以看出,状态转移一共有 4种情况。
从上述分析之后,可以定义状态转移方程如下:

- $dfs(i, 0) = max(dfs(i-1, 0), dfs(i-1, 1) + prices[i])$
- $dfs(i,1) = max(dfs(i-1,1), dfs(i-1,0)-prices[i])$
递归边界:

补充:也可以将i = 0 的情况当成递归边界,但是这样写 需要保证prices数组不为空。若是将i = -1的情况当成递归边界,这样prices数组为空也是可以的,这样写适用性更广。
递归入口:
- 递推公式:$max(dfs(n-1, 0), dfs(n-1, 1)) = dfs(n-1, 0)$
- 递推入口有两种情况:最后一天持有股票 和 最后一天不持有股票。不过仔细推敲,如果最后一天持有股票,那么这个股票卖不出去,这样是亏钱的,所有最优一天不持有股票的情况是较优选中
复杂度分析:
将上述的递归写法 一对一翻译成 递推写法:

进一步优化:
- 由于上边递推式子可以看出,$f[i][status]$ 只依赖于 $f[i-1][status]$两个变量,所以可以用一个长为 2 的数组来表示,这种优化技巧也称为滚动数组优化
- 时间复杂度:O(n),空间复杂度:O(1)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
class Solution {
public:
// 法一:递归搜索
int maxProfit(vector<int>& prices) {
int n = prices.size();
// error: default initialization of an object of const type 'const int'
// 记得 const常量要在 定义的时候就初始化
const int inf = 0x3f3f3f3f;
// memset(inf, 0x3f, sizeof(inf));
/**
* 参数 i : 表示第几天
* 参数 status : 表示当前天数是否 持有股票,1代表持有,0代表不持有
*/
std::function<int(int, int)> dfs = [&](int i, int status) -> int {
if(i < 0)
return status == 1 ? -(inf) : 0;
if(status){
return max(dfs(i - 1, 1), dfs(i - 1, 0) - prices[i]);
} else{
return max(dfs(i - 1, 0), dfs(i - 1, 1) + prices[i]);
}
};
return dfs(n-1, 0);
}
// 法二:记忆化搜索
int maxProfit1(vector<int>& prices) {
int n = prices.size();
const int inf = 0x3f3f3f3f;
int memo[n][2];
// -1表示还没有计算过
memset(memo, -1, sizeof(memo));
std::function<int(int, int)> dfs = [&](int i, int status) -> int{
if(i < 0)
return status == 1 ? -(inf) : 0;
int &res = memo[i][status];
if(res != -1) return res;
if(status)
// 第一种情况:第i-1天 就持有股票,第i天 无交易
// 第二种情况:第i-1天 没持有股票,第i天才 买入股票prices[i]
return res = max(dfs(i - 1, 1), dfs(i - 1, 0) - prices[i]);
else
return res = max(dfs(i - 1, 0), dfs(i - 1, 1) + prices[i]);
};
return dfs(n-1, 0);
}
// 法三:递归 翻译成 递推
int maxProfit2(vector<int>& prices) {
int n = prices.size();
const int inf = 0x3f3f3f3f;
int f[n+1][2];
f[0][0] = 0, f[0][1] = -(inf);
// 注意:这里的f[i][0]表示从第1天到第i天 第i天没有持有股票时的利润
// f[i][1] 表示从第1天到第i天 第i天持有股票时的利润
// 但是prices[i]代表的是 第i天的股票价格,这是从第0天开始计算的,所以股票价格的第0天对应着状态表示的第1天
for(int i = 1; i <= n; ++i){
f[i][0] = max(f[i-1][0], f[i-1][1] + prices[i-1]);
f[i][1] = max(f[i-1][1], f[i-1][0] - prices[i-1]);
}
return f[n][0];
}
// 法四:空间优化,由于上边递推式子可以看出,f[i][status] 只依赖于 f[i-1][status]两个变量
// 所以可以用一个长为二的滚动数组来表示即可
int maxProfit3(vector<int>& prices) {
const int inf = 0x3f3f3f3f;
int f0 = 0, f1 = -(inf);
for(int price : prices){
//1. 计算 从开始日期 到 第i天 没有持有股票状态收益
// - 第i-1天 也没有持有股票,此时第 i 天无交易操作
// - 第i天,持有股票,此时第 i 天将股票卖出
int new_f0 = max(f0, f1 + price);
//2. 计算 从开始日期 到 第i-1天 持有股票状态收益
// - 第i-1天 持有股票,此时第 i 天无交易操作
// - 第i-1天 没持有股票,此时第 i 天将股票买入
f1 = max(f1, f0 - price);
// int f1 = max(f1, f0 - price);
// 通过Debug 输出,可以看到每次 f1输出都是0,这说明每次没有起到更新作用
// 但是一开始百思不得其解,后边发现是 每次f1都重新定义了
// cout << f1 << endl;
// cout << "f0: " << f0 << endl;
// 将 tmp 赋值给 第i天 没有持有股票的状态
f0 = new_f0;
}
return f0;
}
};
|
309. 买卖股票的最佳时机含冷冻期
解题思路:
这道题和 122 题唯一不同之处:
满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,无法在第二天买入股票(冷冻期为1天)
- 买入股票 的前一天 不能有卖出股票的操作
注意:
-
边界条件多了 dfs(-2, 0)=0的情况,所以状态空间二维数组可以初始化为$f[n+2][2]$ ,然后真正的状态从下标为2开始,对应prices数组的prices[0]
-
dfs(−2,1) 是访问不到的,所以下面翻译成递推时,无需初始化这个状态(不需要写 $f[0][1]$ = −∞ )
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
class Solution {
public:
// 法一:记忆化搜索
int maxProfit1(vector<int> &prices) {
int n = prices.size(), memo[n][2];
memset(memo, -1, sizeof(memo)); // -1表示 还没有计算过
const int inf = 0x3f3f3f3f;
function<int(int, bool)> dfs = [&](int i, bool hold) -> int {
if(i < 0) return hold ? -(inf) : 0;
int &res = memo[i][hold];
if(res != -1) return res;
if(hold) {
return res = max(dfs(i-1, true), dfs(i-2, false)-prices[i]);
}else{
return res = max(dfs(i-1, false), dfs(i-1, true)+prices[i]);
}
};
return dfs(n - 1, 0);
}
// 法二:递推写法
// 这道题和 122 题唯一不同之处:
// 满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
// - 卖出股票后,无法在第二天买入股票(冷冻期为1天)
// - 买入股票 的前一天 不能有卖出股票的操作
int maxProfit(vector<int>& prices) {
int n = prices.size();
const int inf = 0x3f3f3f3f;
int f[n+2][2];
memset(f, 0, sizeof(f));
f[1][1] = -(inf); // 现在的 f[1][1] 对应着 i = -1情况
// f[0][1] = -(inf);
// 注意,dfs(−2,1) 是访问不到的,所以下面翻译成递推时,无需初始化这个状态(不需要写 f[0][1]=−∞ )
// 由于 存在冷冻期 所以这里的 买入股票需要 向后回退两个状态,所以将起始天数挪到i = 2位置
// 同时注意:这里由于 f数组 向后挪动两格,对应prices时 下标需要-2
// 注意!!! 一开始 总是没能过样例,原来是 将f状态后移两格之后 在循环迭代需要遍历到 下标为n+1位置
// 一开始循环边界:for(int i = 2; i < n; ++i) 后边的循环边界:for(int i = 2; i < n+2; ++i)
for(int i = 2; i < n+2; ++i){
// 对于卖出股票
f[i][0] = max(f[i-1][0], f[i-1][1] + prices[i-2]);
// 买入操作 必须保证前两天都未持有 股票
// - 允许 001 即过去两天持有股票数为0,今天买入股票
// - 不允许 101
// 操作 f[i-1][0] - prices[i-1] 修改一下 为:f[i-2][0] - prices[i-1]
f[i][1] = max(f[i-1][1], f[i-2][0] - prices[i-2]);
}
// 由于 数组添加了 最开头两个防止越界的列 但还是返回最后天数没有持有股票的收益
// f[n+2][2] 则 返回 f[n+1][0] ,小心这个数组的下标
return f[n+1][0];
}
};
|
188.买卖股票的最佳时机 IV (至多交易k次)
解题思路:

- $dfs(i, j, 0) = max(dfs(i-1, j, 0), dfs(i-1, j, 1) + prices[i])$
- $dfs(i, j, 1) = max(dfs(i-1, j, 1), dfs(i-1, j-1, 0) - prices[i])$
递归边界:

递归入口:
- $max(dfs(n-1, k, 0), dfs(n-1, k, 1)) = dfs(n-1, k, 0)$
注:这道题与上边的买卖股票不同,做出以下的限制
- 不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)- 这个和之前一样
- 最多可以完成
k笔交易(买入股票+卖出股票 算是一笔交易)
注:
- 由于最后未持有股票,手上的股票一定会卖掉,所以代码中的
j-1 可以是在买股票的时候,也可以是在卖股票的时候,这两种写法都是可以的。
- 状态$f[n, k, 0]$ 表示 截止第n天没有持有股票,前边至多进行k次交易所获得最大利润
翻译为 递推写法:

恰好/至少交易k次,如何思考?

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Solution {
public:
// 法一:记忆化搜索
int maxProfit(int k, vector<int>& prices) {
int n = prices.size(), memo[n][k+1][2];
memset(memo, -1, sizeof(memo)); // -1表示还没有计算过
const int inf = 0x3f3f3f3f;
function<int(int, int, bool)> dfs = [&](int i, int j, bool hold) -> int {
if(j < 0) return -(inf);
if(i < 0) return hold ? -(inf) : 0;
int &res = memo[i][j][hold];
if(res != -1) return res;
if(hold)
// 买入作为 一次交易;那么卖出 就不用重复计算了(因为买入 和 卖出 一起作为一次交易)
return res = max(dfs(i-1, j, true), dfs(i-1, j-1, false) - prices[i]);
else
return res = max(dfs(i-1, j, false), dfs(i-1, j, true) + prices[i]);
};
return dfs(n-1, k, 0);
}
// 法二:递推写法
int maxProfit1(int k, vector<int>& prices) {
int n = prices.size(), f[n+1][k+2][2];
// 1. 从上边的 递归返回条件来看,j = -1,交易次数<0时,才返回 -(inf)
// 0~k次交易机会 需要从数组下标 1~k+1对应,在前面插入一个状态 j = -1对应数组下标0的情况
// 所以初始化数组 第二维度大小为 k+2
// 2. 第一维度 从上边递归返回条件来看,i = -1,根据是否持有股票返回对应的值
// 1~n 天对应 数组下标1 ~ n,在前面插入一个状态 i = -1 对应数组下标0的情况
// 所以初始化数组 第一维度大小为 n+1
memset(f, -0x3f, sizeof(f)); // 初始化数组所有元素为 负无穷
// f[*][0][*] = -inf 交易次数 = -1 对应第二维度数组下标为0,初始化为负无穷 代表不可能
// f[0][j][0] = 0 j>=1 对于第-1天 没有持有股票边界情况 初始化为0
// f[0][j][1] = -inf 对j>=1 于第-1天 持有股票边界情况 初始化为负无穷 代表不可能
for(int j = 1; j <= k+1; ++j)
f[0][j][0] = 0;
// 填表顺序 从第一维度 再第二维度
for(int i = 0; i < n; ++i)
for(int j = 1; j <= k+1; ++j){
// 对于第一维度 天数来说 数组最开始插入 -1天边界情况 对应 f[0][*][*]
// 所以实际上 第0天 对应数组下标为 f[1][*][*] 而对应股票价格仍然是prices[0]
f[i+1][j][0] = max(f[i][j][0], f[i][j][1] + prices[i]); // 卖出
f[i+1][j][1] = max(f[i][j][1], f[i][j-1][0] - prices[i]); // 买入
}
return f[n][k+1][0];
}
};
|
课后作业
121.买卖股票的最佳时机
123.买卖股票的最佳时机 III
714.买卖股票的最佳时机含手续费
1911.最大子序列交替和
22 区间DP 最长回文子序列 最优三角剖分
学习大纲
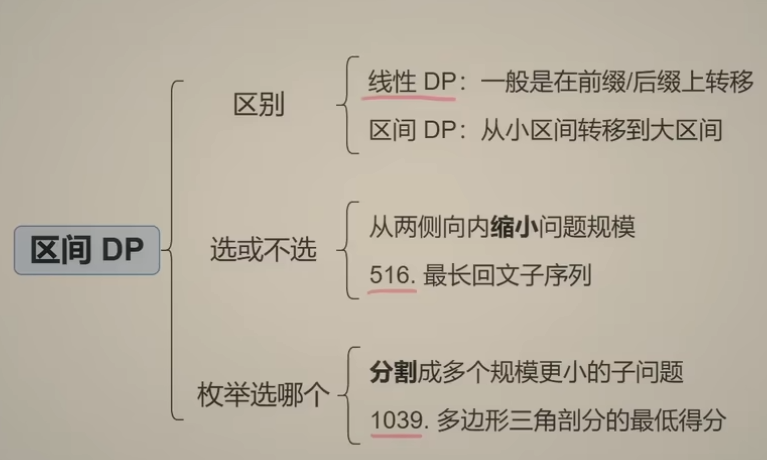
516.最长回文子序列
解题思路:
-
思路一:求 s 和 反转后的s的LCS(最长公共子序列)
-
思路二:子序列,从枚举角度来看,本质上就是==选或不选==的问题,从两侧向内缩小问题规模
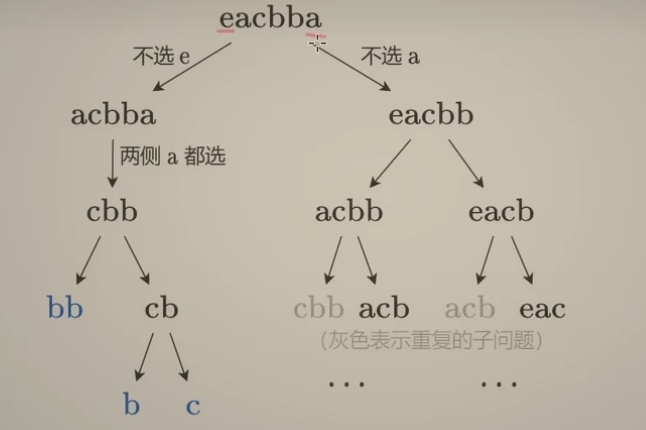
(上边思考方式类似LCS,唯一不同的是 从两侧选字母,相同字母可以都选,不同字母需要只选一个 或者 都不选)
定义$dfs(i, j)$ 表示从 $s[i]$ 到 $s[j]$ 的最长回文子序列的长度
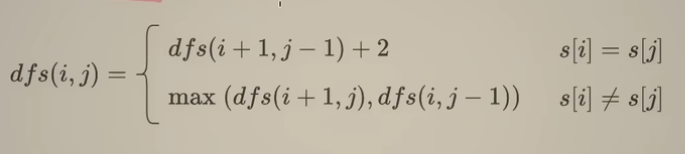
递归边界:
- $dfs(i, i) = 1$
- $dfs(i+1, i)=0$
比如:子序列bb,会出现从$dfs(i, i+1)$ 递归到 $dfs(i+1, i)$ 的情况
递归入口: $dfs(0, n-1)$
**时间复杂度:**状态有$n^2$ 个,每个状态只需要O(1)时间计算,时间复杂度为O($n^2$)
**空间复杂度:**空间复杂度为状态个数,即O($n^2$)
将上述的搜索 翻译成递推写法:

需要上述的状态转移方程中,状态枚举的顺序,这取决于状态生成顺序,从二维数组的==左下角 计算到 右上角==
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
class Solution {
public:
// 法一:递归写法
int longestPalindromeSubseq(string s) {
int n = s.length();
std::function<int(int, int)> dfs = [&](int i , int j) -> int {
if(i > j)
return 0;
if(i == j)
return 1;
if(s[i] == s[j])
return dfs(i+1, j-1) + 2;
return max(dfs(i+1, j), dfs(i, j-1));
};
return dfs(0, n-1);
}
// 法二:记忆化搜索
// - 错误写法(return memo[0][n-1])
// - 正确写法(return dfs(0, n-1))
int longestPalindromeSubseq1(string s) {
int n = s.length();
int memo[n][n];
memset(memo, 0, sizeof(memo)); // 0代表还未初始化,对于i > j的下三角元素来说是初始化
for(int i = 0; i < n; ++i)
memo[i][i] = 1;
// 似乎计算顺序问题 下边这种写法不正确
std::function<int(int, int)> dfs = [&](int i , int j) -> int {
// if(i > j)
// return 0;
// if(i == j)
// return 1;
if(i >= j)
return memo[i][j];
int &res = memo[i][j];
if(res != 0)
return res;
if(s[i] == s[j])
return res = (dfs(i+1, j-1) + 2);
return res = max(dfs(i+1, j), dfs(i, j-1));
};
// return memo[0][n-1]; 这样没有调用dfs 只能返回0
return dfs(0, n-1);
}
// 法二:记忆化搜索 能过版本
int longestPalindromeSubseq2(string s) {
int n = s.length(), memo[n][n];
memset(memo, -1, sizeof(memo)); // -1 表示还没有计算过
function<int(int, int)> dfs = [&](int i, int j) -> int {
if (i > j) return 0; // 空串
if (i == j) return 1; // 只有一个字母
int &res = memo[i][j];
if (res != -1) return res;
if (s[i] == s[j]) return res = dfs(i + 1, j - 1) + 2; // 都选
return res = max(dfs(i + 1, j), dfs(i, j - 1)); // 枚举哪个不选
};
return dfs(0, n - 1);
}
// 法三:翻译成 递推写法
int longestPalindromeSubseq3(string s) {
int n = s.length();
int f[n][n];
memset(f, 0, sizeof(f));
for(int i = n-1; i >= 0; --i){
f[i][i] = 1;
// 这里的 j = i+1 保证了 i < j,并且 i = n-1时,j = n不会进入循环,也就是不会越界访问下边的语句
for(int j = i+1; j < n; ++j){
if(s[i] == s[j]){
f[i][j] = f[i+1][j-1] + 2;
}else{
f[i][j] = max(f[i+1][j], f[i][j-1]);
}
}
}
return f[0][n-1];
}
// 法四:空间优化为 O(n) 暂时还没有头绪
};
|
1039.多边形三角剖分的最低得分
解题思路:
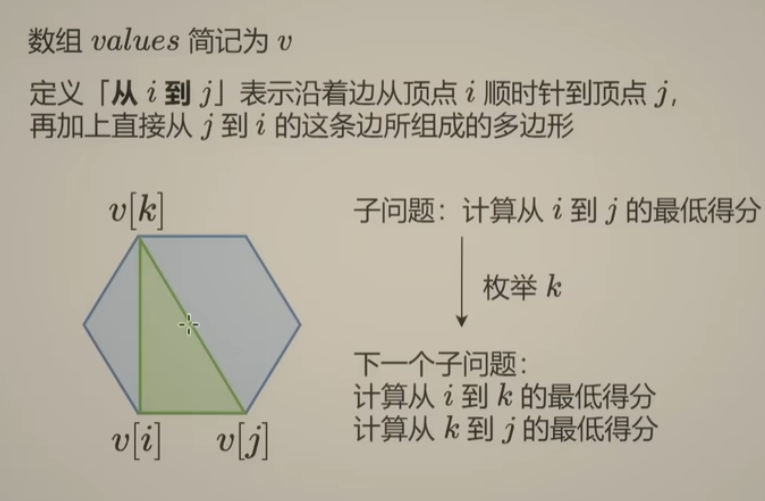
定义 $dfs(i, j)$表示从 i到j这个多边形的最低得分
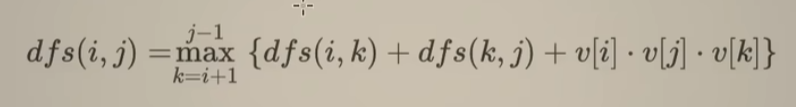
递归边界: $dfs(i, i+1) = 0$
递归入口: $dfs(0, n-1)$
时间复杂度:由于状态有 O($n^2$)个,每个状态需要O(n)时间来计算,故复杂度为O($n^3$)
空间复杂度:状态个数,即O($n^2$)
翻译成递推写法:

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
class Solution {
public:
// 法一:递归写法
// 超时
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
const int inf = 0x3f3f3f3f;
std::function<int(int, int)> dfs = [&] (int i, int j) -> int {
if(i+1 == j)
return 0;
int res = inf;
for(int k = i+1; k < j; ++k)
res = min(res, dfs(i, k)+dfs(k, j)+ values[i]*values[j]*values[k]);
return res;
};
return dfs(0, n-1);
}
// 法二:记忆化搜索
int minScoreTriangulation1(vector<int>& values) {
int n = values.size();
const int inf = 0x3f3f3f3f;
int memo[n][n];
// 初始化每个元素为 inf,表示还未填充
memset(memo, 0x3f, sizeof(memo));
std::function<int(int, int)> dfs = [&](int i, int j) ->int {
if(i+1 >= j)
return 0;
int& res = memo[i][j];
if(res != inf)
return res;
// 注意:k的取值为[i+1, j-1]
for(int k = i+1; k < j; ++k)
// 由于这下边 要去min最小值,所以需要定义res一开始为inf,否则res=0总是最小值
res = min(res, dfs(i, k)+dfs(k, j)+values[i]*values[j]*values[k]);
return res;
};
return dfs(0, n-1);
}
// 法三:翻译成 递推写法
int minScoreTriangulation2(vector<int>& values){
int n = values.size();
int f[n][n];
const int inf = 0x3f3f3f3f;
memset(f, 0, sizeof(f));
// 注意:i < k,f[i]由f[k]转移过来 需要倒序枚举
// j > k,f[i][j]由f[i][k]转移过来 需要正序枚举
// i, k, j至少围成一个三角形,也就是 j至少要从i+2开始,所以i 倒序枚举从n-3开始
for(int i = n-3; i >= 0; --i)
for(int j = i+2; j < n; ++j){
int res = inf;
for(int k = i+1; k < j; ++k)
res = min(res, f[i][k]+f[k][j]+values[i]*values[j]*values[k]);
f[i][j] = res;
}
return f[0][n-1];
}
};
|
课后作业
375.猜数字大小 II
132.分割回文串 II
1312.让字符串成为回文串的最少插入次数
1771.由子序列构造的最长回文串的长度
1547.切棍子的最小成本
1000.合并石头的最低成本
23 树形DP(1) 树的直径
学习大纲:

543.二叉树的直径
解题思路:
-
二叉树直径定义:指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
-
复习:二叉树的最大深度

-
换个角度看直径:
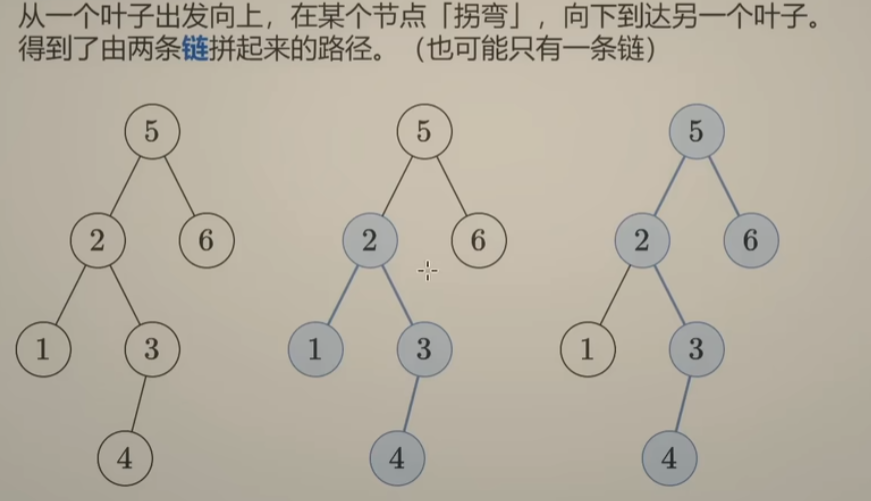
从这样看:最大直径 = 左子树最大深度 + 右子树最大深度 + 2
-
算法:
遍历整棵二叉树,==在计算最长链的同时==,顺带把直径算出来
在当前结点 [拐弯] 的直径长度 = 左子树的最长链 + 右子树的最长链 + 2
而==以当前结点为根的子树最长链==计算公式如下:
返回给父节点 是以当前节点为根的子树的最长链 = Max(左子树的最长链,右子树的最长链) + 1
-
时间复杂度:每个结点都遍历一遍,时间复杂度为O(n)
-
空间复杂度:最坏情况下,二叉树是一条链,递归需要O(n)的栈空间
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
int ans = 0;
std::function<int(TreeNode *)> dfs = [&](TreeNode *root) -> int{
if(root == nullptr)
return -1;
// 返回值为最大深度
int l_len = dfs(root->left);
int r_len = dfs(root->right);
// 计算每个节点的链长,并且更新全局变量ans
ans = max(ans, l_len + r_len + 2);
return max(l_len, r_len) + 1;
};
dfs(root);
return ans;
}
private:
// 链长 计算需要用到最大深度,而函数的返回值为最大深度
// 可以传入一个全局变量,这样在递归的时候就可以计算每个节点的链长
// 取所有节点链长的最大值 为最大深度
int longestDepth(TreeNode* root) {
// 叶子节点最长链为0,叶子节点的左右子节点为 虚拟节点 最长链为-1
if(root == nullptr)
return -1;
return max(longestDepth(root->left), longestDepth(root->right)) + 1;
}
};
|
124.二叉树中的最大路径和
解题思路:
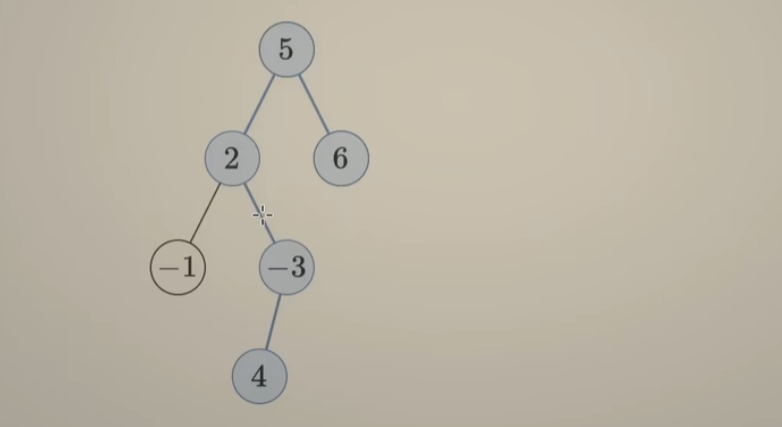
-
算法: 遍历二叉树,在计算最大链和的同时,顺带更新答案的最大值
当前结点 [拐弯] 的最大路径和 = 左子树最大链和 + 右子树最大链和 + 当前节点值
返回给父节点(函数返回值):max(左子树最大链和,右子树最大链和) + 当前节点值
注意:==如果返回值为负数==,则返回0
-
时间复杂度:O(n)
-
空间复杂度:O(n)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
int maxPathSum(TreeNode* root) {
const int inf = 0x3f3f3f3f;
// 由于节点值 有负数,且路径上至少要有一个点,答案可以 初始为 负无穷大
int val = -(inf);
std::function<int(TreeNode*)> dfs = [&] (TreeNode *root) -> int{
if(root == nullptr)
return 0;
int l_val = dfs(root->left);
int r_val = dfs(root->right);
// 更新全局的 路径和
val = max(val, l_val+r_val+root->val);
// return (max(l_val, r_val) + root->val < 0) ? 0 : max(l_val, r_val) + root->val;
return max(max(l_val, r_val)+root->val, 0);
};
dfs(root);
return val;
}
};
|
2246.相邻字符不同的最长路径
解题思路:
-
引入邻居概念:如果两个点 x 与 y之间有边相连,可以说 x是y的邻居,y是x的邻居
-
两种思路如下:

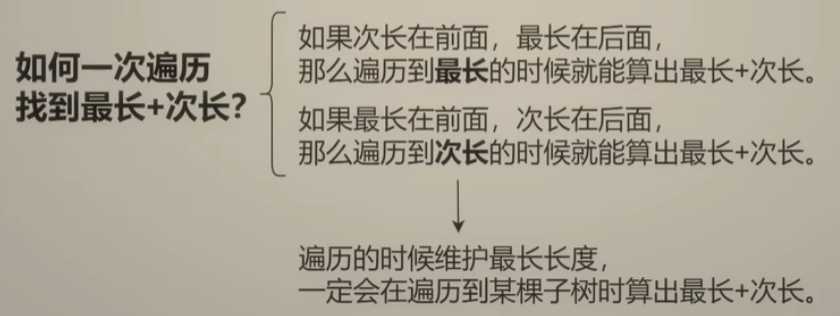
-
代码思路详剖:
-
枚举子树 x 的所有子树 y ,维护从 x 出发的最长路径 maxLen,那么可以更新答案为从 y 出发的最长路径加上 maxLen,再加上 1(边 x−y),即合并从 x 出发的两条路径。递归结束时返回maxLen。
对于本题的限制,我们可以在从子树 y 转移过来时,==仅考虑从满足 s[y]≠s[x]的子树 y 转移过来==,所以对上述做法加个 if 判断就行了。
-
时间复杂度:O(n)
-
空间复杂度:O(n)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
class Solution {
private:
map<int, vector<int>> mp;
public:
// 思路二:遍历x的子树的同时 求最大+次长
// 注意:思路可行,但是运行超时 通过样例比例 138/142 后边改了变量名 居然勉强能过???
int longestPath(vector<int>& parent, string s) {
int n = parent.size();
// 0是根结点 边不存在,其余结点与根结点有边 或者 其余结点之间有边
for(int i = 1; i < n; ++i){
mp[parent[i]].push_back(i);
}
int ans = 0;
// 注:这道题的 最长路径 指的是 路径上结点的个数
// 而函数 返回值为 路径长度
// 结点个数 = 路径长度 + 1
std::function<int(int)> dfs = [&] (int x) ->int {
// int x_len = 0;
int maxLen = 0;
// map容器 使用迭代器访问
// 报错:No viable conversion from 'std::pair<const int, int>' to
// 'map<int, int>::iterator' (aka '_Rb_tree_iterator<std::pair<const int, int>>')
// for(auto it : mp) {
//
// }
// 这里 x为 根结点下标,y为 孩子结点下标
vector<int> vi = mp[x];
for(int y : vi) {
// int y_len = dfs(y) + 1;
int len = dfs(y) + 1;
if(s[y] != s[x]) {
// ans = max(ans, x_len+y_len);
ans = max(ans, maxLen + len);
// 更新最长的子结点 路径
maxLen = max(maxLen, len);
// x_len = max(x_len, y_len);
}
}
return maxLen;
};
// 注:如果 x的邻居包含 父节点,可以额外传入 父节点fa
std::function<int(int, int)> dfs1 = [&] (int x, int fa) ->int {
int x_len = 0;
// map容器 使用迭代器访问
// 报错:No viable conversion from 'std::pair<const int, int>' to
// 'map<int, int>::iterator' (aka '_Rb_tree_iterator<std::pair<const int, int>>')
// for(auto it : mp) {
//
// }
// 这里 x为 根结点下标,y为 孩子结点下标
vector<int> vi = mp[x];
for(int y : vi) {
if(y == fa) continue;
int y_len = dfs1(y, x) + 1;
if(s[y] != s[x]) {
ans = max(ans, x_len+y_len);
// 更新最长的子结点 路径
x_len = max(x_len, y_len);
}
}
return x_len;
};
dfs1(0, -1);
// dfs(0);
return ans+1;
}
// dfs函数 解释:
// maxLen 表示遍历过的父、子间的最长路径,len 表示当前这一条路径长度,
// 遍历一遍后,可以覆盖所有情况;最终找到父到最长的两个子的路径长度和
};
|
课后作业
687.最长同值路径
1617.统计子树中城市之间最大距离
2538.最大价值和与最小价值和的差值
24 树形DP(2) 打家劫舍III 树上最大独立集
回顾:上期学习了,树形DP中的树的直径,下边学习两种树形DP — 树上最大独立集 和 树上最小支配集
337.打家劫舍 III
解题思路:
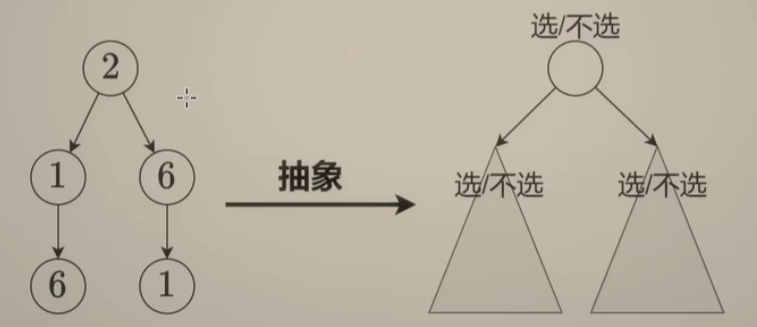
分类讨论:
- 根结点2选择,那么与根结点相连的 两个子节点都不可以选
- 根结点2 不选择,那么与根结点相连的 两个子节点可以 选/不选
回顾之前 数组版本的打家劫舍:选或不选的思路,如果不选第i个数,那么从第i-1个数转移过来;如果选第i个数,那么从i-2个数转移过来。
如果照搬上边的思路,比如:==当前选了根结点==,此时儿子结点不能选,那么就需要从儿子的儿子结点转移过来,这样考虑 ==至多需要考虑四个孙子结点==,并且没考虑一个结点都要判断儿子是否为空、孙子是否为空,非常繁琐复杂。
重新思考:能不能直接从 儿子结点状态转移过来?
- 每个节点 都有 选 或 不选 两种情况,将这两种情况当作两个状态
将上述想法转换如下:

- 时间复杂度:由于每个结点 只递归一次,所以复杂度为O(n)
- 空间复杂度:在最坏情况下,这棵二叉树是一条链,递归需要O(n)的栈空间,所以空间复杂度为O(n)
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
int rob(TreeNode* root) {
std::function<vector<int>(TreeNode*)> dfs = [&] (TreeNode* node) -> vector<int> {
if(node == nullptr)
return {0, 0}; // 选, 不选
vector<int> left = dfs(node->left);
vector<int> right = dfs(node->right);
// 偷 根结点房子 那么不能偷左右节点
int rob = left[1] + right[1] + node->val;
// 不偷 根结点房子 那么可以偷左右节点房子,也可以不偷左右节点房子,取最大效益方案
int not_rob = max(left[0], left[1]) + max(right[0], right[1]);
return {rob, not_rob};
};
vector<int> ans = dfs(root);
// 答案是 根结点 选或不选的最大值
return max(ans[0], ans[1]);
}
};
// 灵神写法
class Solution1 {
pair<int, int> dfs(TreeNode *node) {
if (node == nullptr) // 递归边界
return {0, 0}; // 没有节点,怎么选都是 0
auto [l_rob, l_not_rob] = dfs(node->left); // 递归左子树
auto [r_rob, r_not_rob] = dfs(node->right); // 递归右子树
int rob = l_not_rob + r_not_rob + node->val; // 选
int not_rob = max(l_rob, l_not_rob) + max(r_rob, r_not_rob); // 不选
return {rob, not_rob};
}
public:
int rob(TreeNode *root) {
// 结构化绑定写法
auto [root_rob, root_not_rob] = dfs(root);
return max(root_rob, root_not_rob); // 根节点选或不选的最大值
}
};
|
总结
最大独立集 和 树上最大独立集的关系

若是 每棵树的点权都为1,则求的就是最大独立集。
树形DP如何思考?
常见的套路:
- 选或不选
- 枚举选哪个
课后作业
没有上司的舞会
上述做题思路可以推广到一般树上,如果选当前结点,它的儿子都不能选;如果不选当前结点,每个儿子都可以考虑 选/不选,取最值。公式如下:
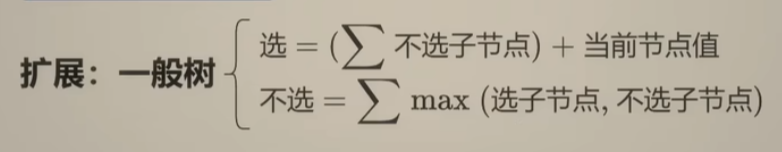
1377.T 秒后青蛙的位置
1377 思考题:如果有多个目标位置呢?
2646.最小化旅行的价格总和
(会员题)https://leetcode.cn/problems/choose-edges-to-maximize-score-in-a-tree/
https://codeforces.com/problemset/problem/1689/C
25 树形DP(3) 监控二叉树 树上最小支配集
968.监控二叉树
解题思路:
原题:给定一个二叉树,在树的节点上安装摄像头。节点上的每个摄像头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。

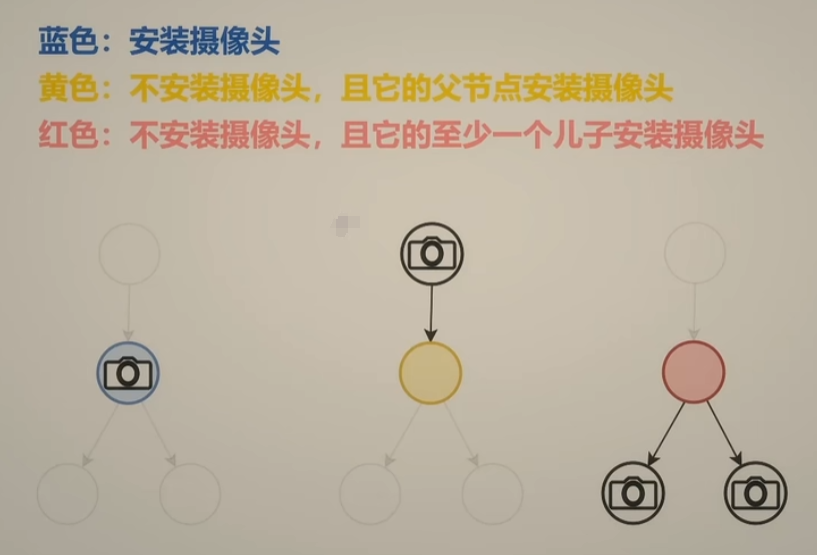
注:一个节点的父节点 和 儿子节点都安装了摄像头,那么它即可以是黄色节点,也可以是红色节点。
1、分类讨论如下:
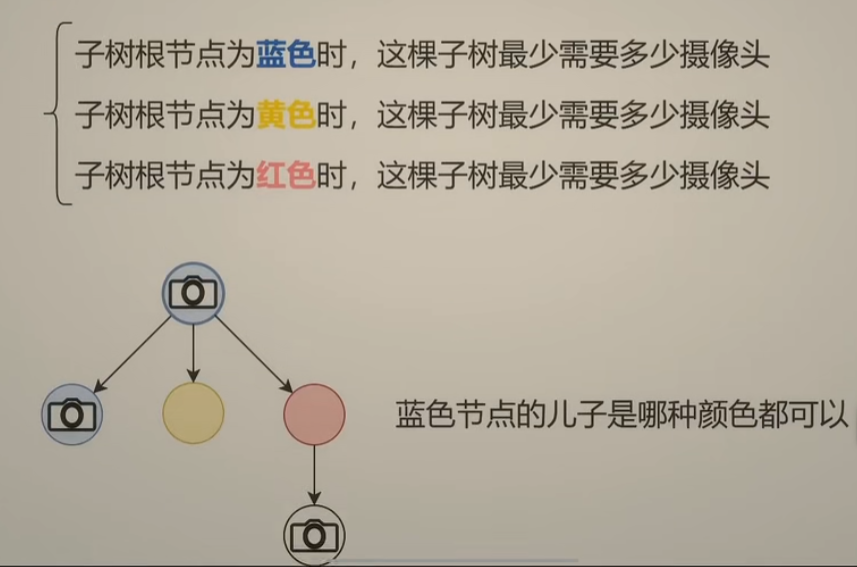
根结点为蓝色公式:蓝色 = min(左蓝,左黄,左红) + min(右蓝,右黄,右红) + 1
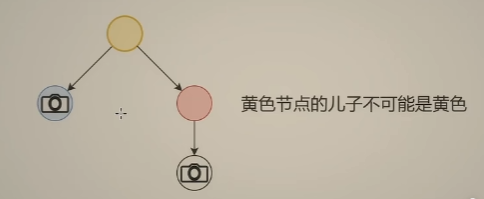
根结点为黄色公式:黄色 = min(左蓝,左红) + min(右蓝,右红)
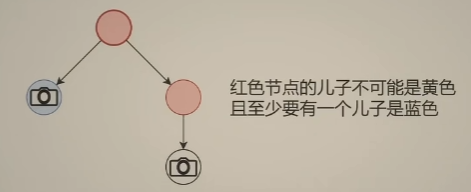
根结点为红色公式:红色 = min(左蓝+右红,左红+右蓝,左蓝+右蓝)
2、整棵树根结点情况:
由于二叉树的根结点没有父节点,不可能是 黄色,所以:
最终答案 = min(根节点为蓝色,根节点为红色)
3、递归边界考虑:

时间复杂度:递归整棵二叉树,每个节点递归一次,时间复杂度为O(n)
空间复杂度:最坏情况下,这棵二叉树会形成一条链,递归所需的栈空间为O(n)
变形1: 在节点x安装摄像头,需要花费cost[x],求监控所有节点的最小花费是多少?(上述监控二叉树,相当于把每个节点安装摄像头 花费为1)
将上述公式中,选择当前节点公式中的1改成 当前节点安装摄像头花费cost[x]即可,如下:
int choose = min(l_choose, min(l_by_fa, l_by_children)) + min(r_choose, min(r_by_fa, r_by_children)) + cost[x];
**变形2:**如果一个红色节点有3个儿子呢? 有4个儿子呢?
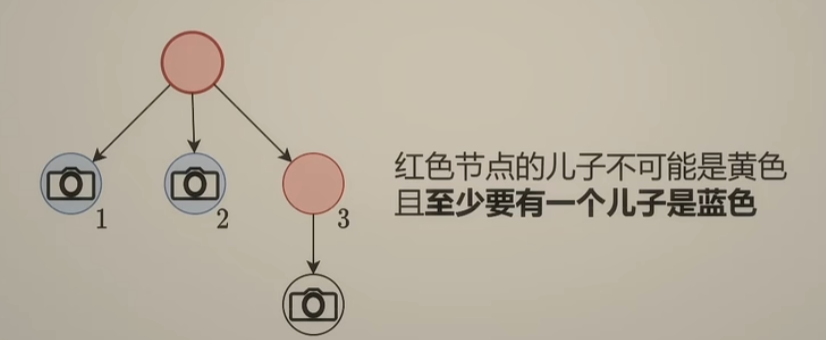
可以发现公式中讨论情况很多,如下:

最后得到化简后的式子:

完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
private:
tuple<int, int, int> dfs(TreeNode *node) {
if(node == nullptr) {
return {INT32_MAX/2, 0, 0}; // 除2 防止加法溢出
}
// 结构化绑定 + 搭配 tuple使用
auto [l_choose, l_by_fa, l_by_children] = dfs(node->left);
auto [r_choose, r_by_fa, r_by_children] = dfs(node->right);
int choose = min(l_choose, min(l_by_fa, l_by_children)) + min(r_choose, min(r_by_fa, r_by_children)) + 1;
int by_fa = min(l_choose, l_by_children) + min(r_choose, r_by_children);
int by_children = min(l_choose+r_by_children, min(l_by_children+r_choose, l_choose+r_choose));
return {choose, by_fa, by_children};
}
public:
int minCameraCover(TreeNode* root) {
auto [choose, _, by_children] = dfs(root);
return min(choose, by_children);
}
};
// 灵神写法:使用化简后的公式进行计算 速度更快
class Solution1 {
tuple<int, int, int> dfs(TreeNode *node) {
if (node == nullptr) {
return {INT32_MAX / 2, 0, 0}; // 除 2 防止加法溢出
}
auto [l_choose, l_by_fa, l_by_children] = dfs(node->left);
auto [r_choose, r_by_fa, r_by_children] = dfs(node->right);
int choose = min(l_choose, l_by_fa) + min(r_choose, r_by_fa) + 1;
int by_fa = min(l_choose, l_by_children) + min(r_choose, r_by_children);
int by_children = min({l_choose + r_by_children, l_by_children + r_choose, l_choose + r_choose});
return {choose, by_fa, by_children};
}
public:
int minCameraCover(TreeNode *root) {
auto [choose, _, by_children] = dfs(root);
return min(choose, by_children);
}
};
|
课后作业
保安站岗 https://www.luogu.com.cn/problem/P2458
保安站岗 Python 代码 https://www.luogu.com.cn/paste/y9iiynzw
保安站岗 Go 代码 https://www.luogu.com.cn/paste/ei5ihtp6
LCP34. 二叉树染色(选做) https://leetcode.cn/problems/er-cha-shu-ran-se-UGC/
LCP64. 二叉树灯饰(选做) https://leetcode.cn/problems/U7WvvU/
26 单调栈 每日温度 接雨水
739.每日温度
解题思路:
题意:假设有一张 每日温度的折线图,这里的数字表示每一天温度。请你计算每一天的一个更大温度 出现在几天后?
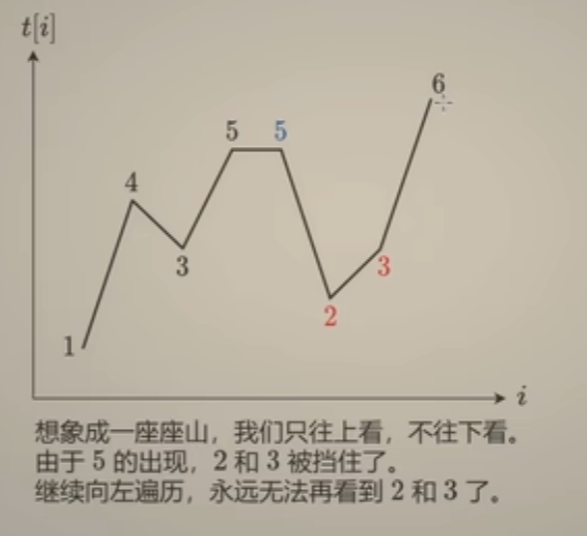
-
暴力做法:比如从上边温度为5的下一个数开始,向右一个一个地遍历,直到找到一个大于5的数,最坏情况下(所以元素都一样),需要花费O($n^2$)时间
-
优化(==从右到左==的思路):承接上边图片说明文字,分类讨论:
- 对于比 2 小的数,例如前边的1,由于5出现,==2不可能成为1的下一个更大的数==
- 对于大于等于2的数,比如前边的3,==2更不可能成为其下一个更大的数==
结论:由于5的出现,2或者3不可能 作为5 左侧某个数的下一个更大的数,那就可以放心把 2和3去掉,不去遍历这两个数。

由于 在记录一个数时,会把所有$\leq$ 这个数的数据从栈中弹出,不可能出现栈中数据:上面大下面小的情况,这说明栈中存储的数据是有序的,所以这个数据结构也叫做单调栈。
-
时间复杂度:每个元素只会入栈一次,出栈至多一次,所以循环代码至多执行n次,复杂度为O(N)
-
空间复杂度:最坏情况下,栈里边有n个元素,复杂度为O(n),不过考虑到本地值域很小 $30 \leq temperatures[i] \leq 100$,栈中最多只有71个元素,所以复杂度也可以为O(min(n, U)) (其中 U = max-min+1),常数级别。
-
优化(==从左到右==思路):从左往右扫描数组,元素1入栈,接着元素4,由于4>1,比1大的元素已经找到,不需要存到栈中,出栈,此时元素4入栈。接着扫描3,入栈;扫描5,此时5>3 且 5 > 4,所以栈中元素向左搜索更大的数即为5,不用存储在栈中,出栈,此时5入栈,以此类推。
- 可以看到,**从左到右写,站里面存储的数还没有找到下一个更大的数,一旦发现一个比栈顶更大的数,**就==立刻更新栈顶的答案==,同时把栈顶元素出栈。
小结:上边两种不同的思路,其实是看待同一个问题的不同角度。可以把下一个更大的数存到栈中(从右到左思路),也可以反过来,把没有找到下一个更大的数的那些数存到栈里边(从左到右思路)。用16个字总结一下单调栈的两种写法:及时去掉无用数据,保证栈中数据有序
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
class Solution {
public:
// 法一:利用单调栈 单调递减规律求解(自己思考 30分钟+20分钟Debug)
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> ans(n, 0);
// pair<int, int> 第一个int表示 数组元素,第二个int表示 元素在温度数组的下标
stack<pair<int, int>> st; // 维护一个 单调栈 栈内元素单调递减
// 顺序遍历 温度数组,每个元素入栈,下一个元素入栈之前 检查是否符合单调递减
// 若符合:暂时没有找到 入栈之前 栈顶元素的 下一个更大值隔阂天数
// 若不符合,栈顶元素出栈,找到栈顶元素从左到右数数 碰到的第一个最大值
pair<int, int> tmp;
for(int i = 0; i < n; ++i){
// 如果栈不为空
if(!st.empty()){
tmp = st.top();
// 如果下边没有判断 st.empty() 栈是否为空,会报以下可能错误:
// runtime error: reference binding to misaligned address 0xbebebebebebec0b6 for type 'std::pair<int, int>',
// which requires 4 byte alignment (stl_deque.h)
while(tmp.first < temperatures[i]){
ans[tmp.second] = i - tmp.second;
st.pop();
if(st.empty()) break;
tmp = st.top();
}
// st.push(make_pair(temperatures[i], i));
}
st.push(make_pair(temperatures[i], i));
}
return ans;
}
// 法二:单调栈 Up思路
// 从右到左的思路
vector<int> dailyTemperatures1(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> ans(n, 0);
stack<int> st;
for(int i = n-1; i >= 0; --i){
int t = temperatures[i];
while(!st.empty() && t >= temperatures[st.top()])
st.pop();
if(!st.empty()){
ans[i] = st.top() - i;
}
st.push(i);
}
return ans;
}
// 法三:单调栈 Up思路
// 从左到右的思路
// 注:从左到右计算 更可以体现单调栈的性质:一旦当前遍历温度t <= 栈顶元素
// 可以推出,t同时也小于等于栈里面任意数,所以当t <= 栈顶元素
// 意味着 t无法更新栈顶,也无法更新栈里面任何元素(的答案) 因为栈是单调的
vector<int> dailyTemperatures2(vecotr<int>& temperatures){
int n = temperatures.size();
vector<int> ans(n, 0);
stack<int> st;
for(int i = 0; i < n; ++i){
int t = temperatures[i];
while(!st.empty() && t > temperatures[st.top()]){
int j = st.top(); st.pop();
ans[j] = i - j;
}
st.push(i);
}
return ans;
}
};
|
42.接雨水
解题思路:
之前学过接雨水 前后缀分解 和相向双指针做法,都是假设每个位置都有一个水桶。计算每个水桶能接多少水,这样思考是竖着计算。

横着计算思路:从左到右遍历 ,栈中元素 5 2 1 0,如下:
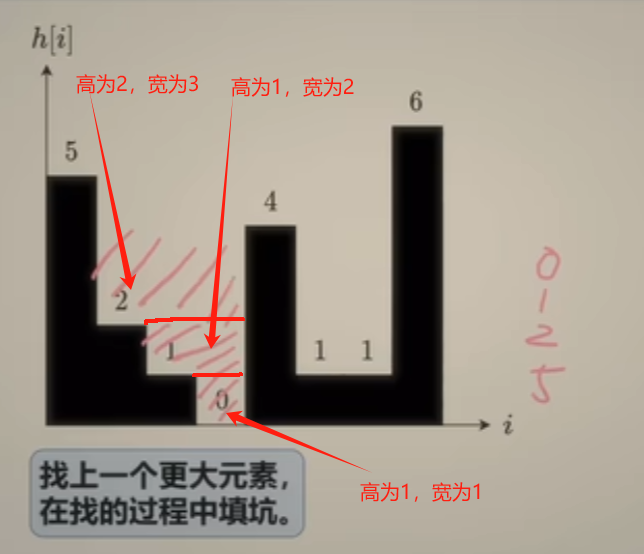
从计算过程可以发现:面积由三个下标决定,即 当前元素下标、栈顶元素下标、栈顶元素下边元素的下标。
例如:栈元素为 5 2 ,此时扫描元素为4时,元素5和4的下标查-1 就是高位2 宽为3区域的长,此时min(5, 4) - 栈顶元素2 就是高位2 宽为3区域的高。
用十六个字总结上述算法:找上一个更大元素,在找的过程中填坑。
时空复杂度:同第一题。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
class Solution {
public:
// 26.单调栈 例题
// 调试了一下下边代码,发现pre和suf数组没出错,不能过样例,后面反思一下 是自己思路有误
// pre[i]含义 应该为 第i根柱子 从右往左数 最后一根比它高的柱子高度
// 解题思路:维护两个单调栈(单调递减) 求两个数组
// 数组 pre[i]:表示第i根柱子 从右往左数 第一根比它高的柱子 高度
// 数组 suf[i]:表示第i根柱子 从左往右数 第一根比它高的柱子 高度
// 如果没有比柱子高的 数组元素值为 第i根柱子本身高度
int trap2(vector<int>& height) {
int n = height.size();
vector<int> pre(height), suf(height);
// pair<int, int> 第一个int表示 数组元素,第二个int表示 元素在温度数组的下标
stack<pair<int, int>> st;
pair<int, int> tmp;
for(int i = 0; i < n; ++i){
if(!st.empty()){
tmp = st.top();
while(tmp.first < height[i]){
suf[tmp.second] = height[i];
st.pop();
if(st.empty()) break;
tmp = st.top();
}
}
st.push(make_pair(height[i], i));
}
while(!st.empty()) st.pop();
for(int i = n-1; i >= 0; --i){
if(!st.empty()){
tmp = st.top();
while(tmp.first < height[i]){
pre[tmp.second] = height[i];
st.pop();
if(st.empty()) break;
tmp = st.top();
}
}
st.push(make_pair(height[i], i));
}
// >>>debug代码
// for(int i = 0; i < n; ++i)
// cout << pre[i] << " ";
// cout << endl;
// for(int i = 0; i < n; ++i)
// cout << suf[i] << " ";
// >>>debug代码
int ans = 0;
for(int i = 0; i < n; ++i){
ans += (min(pre[i], suf[i])-height[i]);
}
return ans;
}
// 26.单调栈 例题
// Up主思路实现
int trap3(vector<int>& height) {
int ans = 0;
stack<int> st;
int n = height.size();
for(int i = 0; i < n; ++i){
int h = height[i]; // 右边柱子高度
while(!st.empty() && h >= height[st.top()]){
int bottom_h = height[st.top()]; // 找中间柱子高度
st.pop();
if(st.empty()) break;
int left = st.top(); // 找左边柱子 下标
int dh = min(h, height[left]) - bottom_h; // 填坑 高度
ans += dh * (i - left - 1);
}
st.push(i);
}
return ans;
}
};
|
小结
如果要计算的内容 涉及到上一个或者下一个更大或更小的元素,可以考虑使用单调栈解决。

课后作业
1475.商品折扣后的最终价格
901.股票价格跨度
1019.链表中的下一个更大节点
1944.队列中可以看到的人数
84.柱状图中最大的矩形
85.最大矩形
27 单调队列 滑动窗口最大值
239.滑动窗口最大值
解题思路:
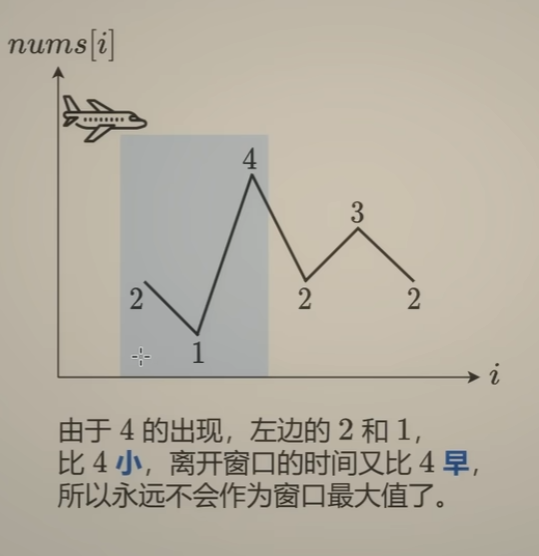
-
暴力解法:枚举每个长为k的连续子数组,对每个子数组遍历找到最大值。如果k = n/2,大约为数组的一半,时间复杂度为O($n^2$)
-
优化解法(单调队列):假设有一架飞机 飞过一排山峰,飞机只能看到视野内的山峰高度,一眼望去就可以看到 视野内最高山峰。
一开始将山峰高度 记录到一个队列中:2 1,接着:由于4的出现,左边的2和1比4小,离开窗口时间比4早,永远不会作为窗口最大值。可以将队列中的2 1出列,然后将4入队列。
从上边例子中可以看出,每次遇到一个数==都把前面比它小的数去掉==,当然如果有相同数字也可以去掉保留最右边那个数,所以 队列中记录的数**从左到右是严格递减的。**那么最大值自然是队列中最左边那个数了。
需要一个什么样的数据结构维护上边的数字?
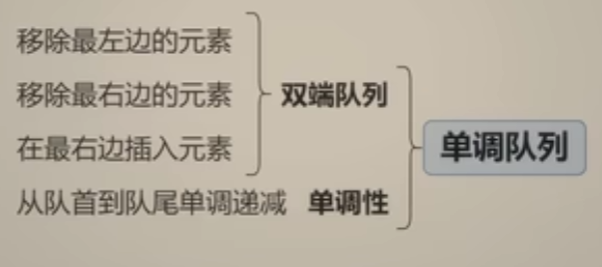
时间复杂度:分析方法类似单调栈。每个下标入队出队最多一次,所以下边二重循环次数最多n次,复杂度为O(n)
空间复杂度:在不考虑返回值ans数组大小情况下,窗口大小为k,双端队列中有O(k)个元素,空间复杂度为O(k)。
- 精确分析,在内循环中,将相同的队尾元素弹出,所以队列中没有相同的数,时间复杂度为 O(min(k, U)),其中$U = len(set(nums))$。例如:题目中指出 $1 \leq k \leq nums.length$,数组长度范围为$10^5$,但是数组的取值 $-10^4 \leq nums[i] \leq 10^4$,所以队列中元素至多为20001个,但是k长度范围为 $10^5$
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> ans;
int n = nums.size();
deque<int> q; // 双端队列
for(int i = 0; i < n; ++i){
int val = nums[i];
//1. 元素进入窗口
while(!q.empty() && nums[q.back()] <= nums[i]){
q.pop_back(); // 将队尾不符合单调性 元素出队,维护q的单调性
}
q.push_back(i); // 当前元素下标入队
//2. 元素出窗口
if(i - q.front() + 1 > k) { // 队首 离开窗口
q.pop_front();
}
//3. 记录答案
if(i >= k-1) { // 窗口最右边游标 开始大于k-1,表示窗口大小符合k
// 由于 队首到队尾单调递减,所以窗口最大值就是队首
ans.push_back(nums[q.front()]);
}
}
return ans;
}
};
|
小结
这里的无用指两个方面:
- 像单调栈一样,在把元素加入队尾之前,根据大小关系,弹出队尾元素
- 当队首元素离开窗口后,也需要及时把它弹出队列
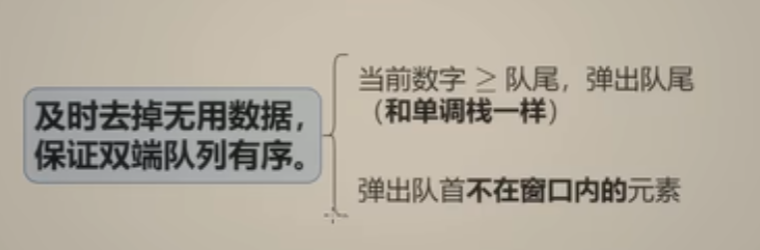
课后作业
1438.绝对差不超过限制的最长连续子数组
2398.预算内的最多机器人数目
862.和至少为 K 的最短子数组
1499.满足不等式的最大值
1696.跳跃游戏 VI
2944.购买水果需要的最少金币数
附录
参考文献
版权信息
本文原载于kitebin.top,遵循CC BY-NC-SA 4.0协议,复制请保留原文出处。









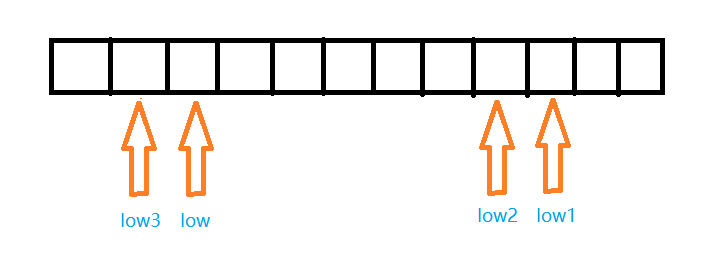

































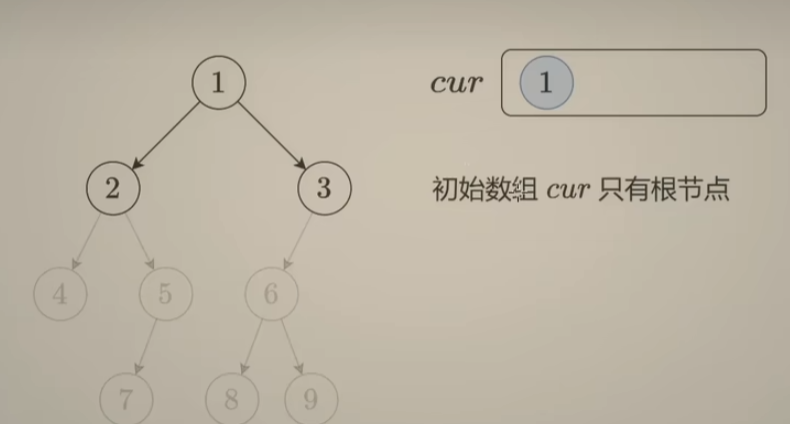
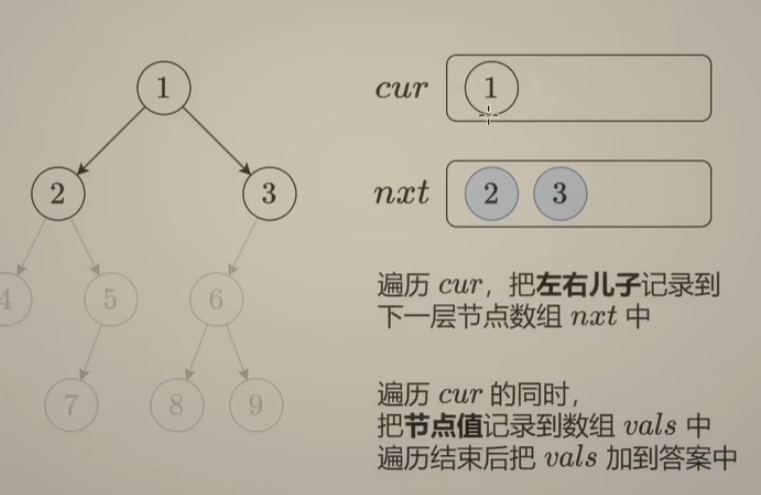
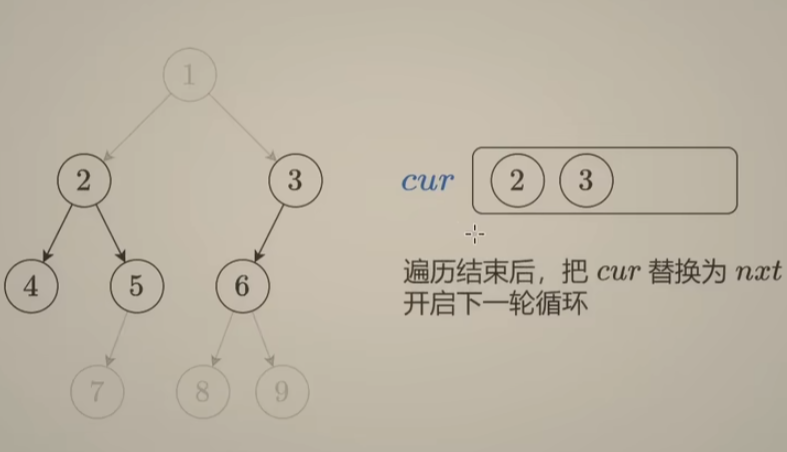
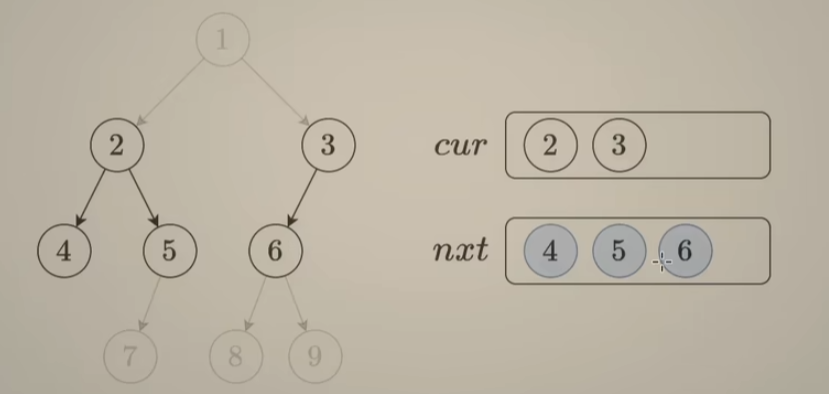
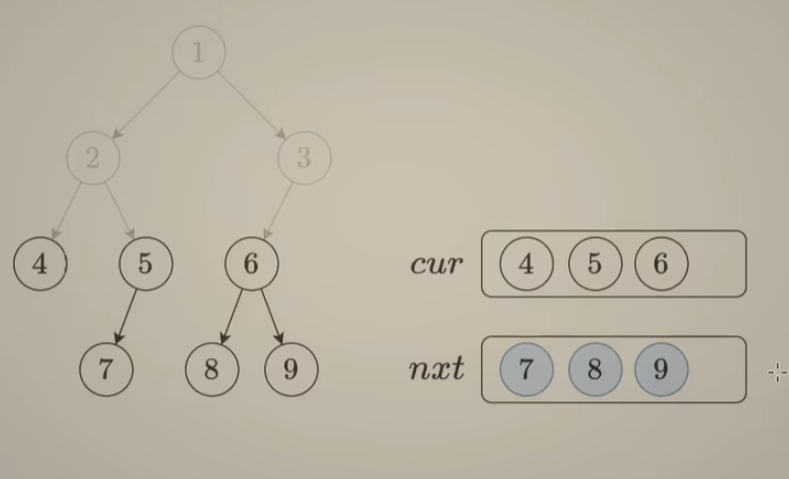
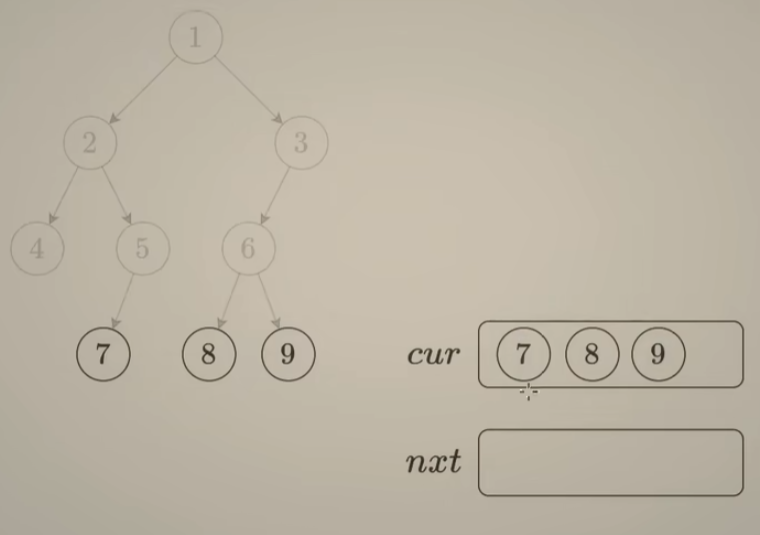
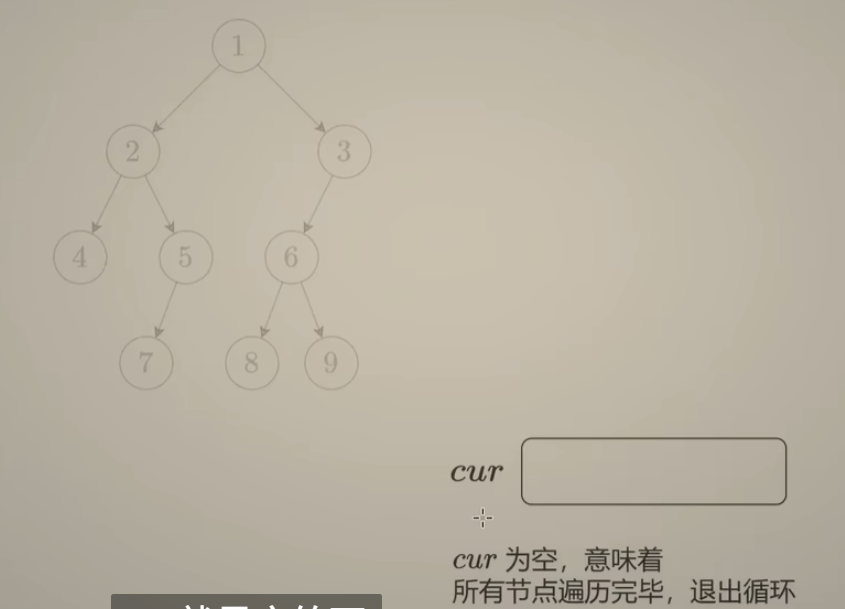

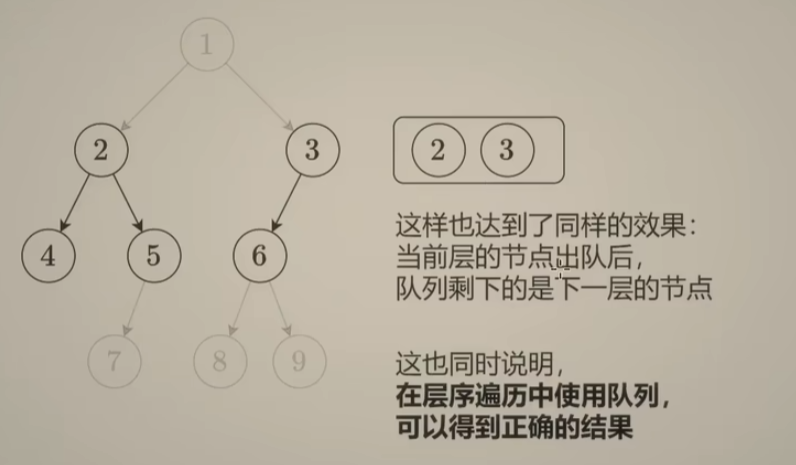
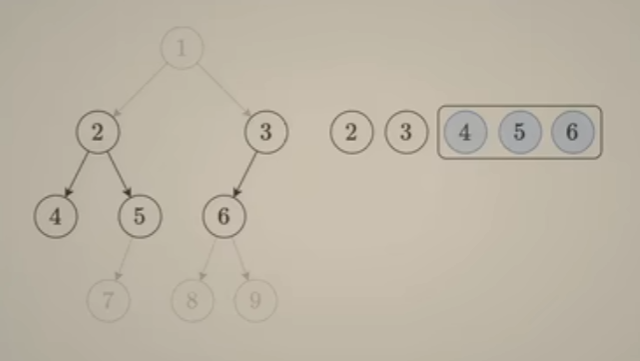
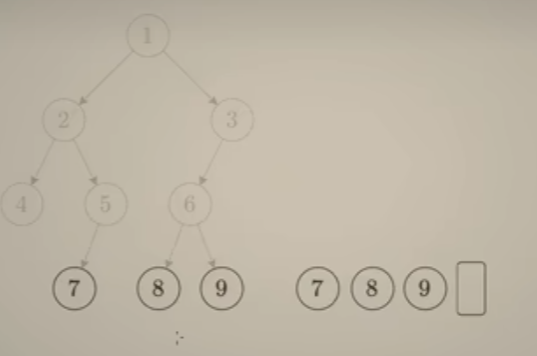









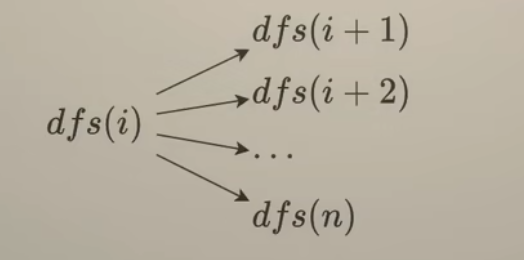

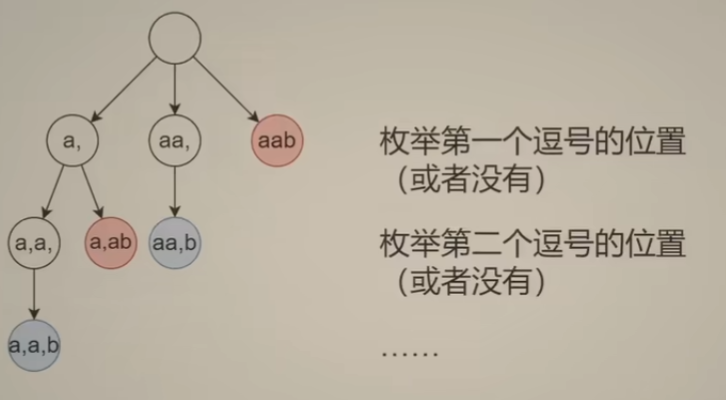









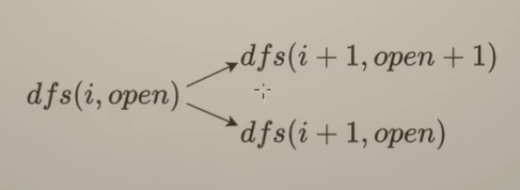






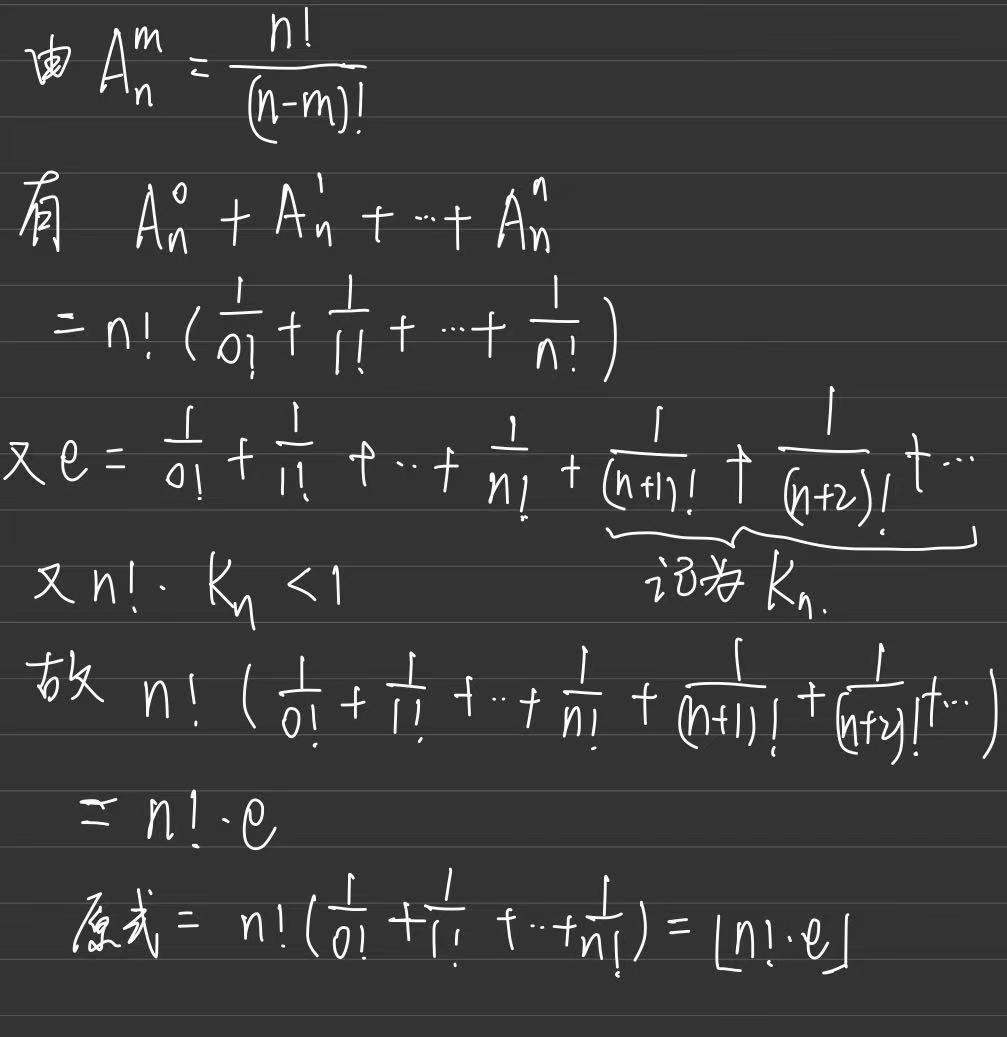



















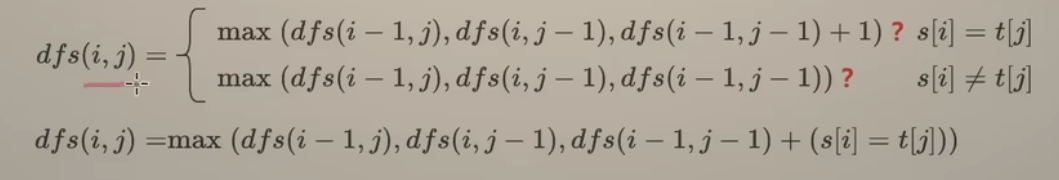

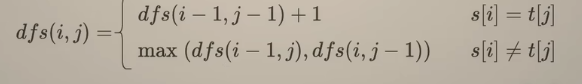


 回溯
回溯